题目
计算曲线积分((2x-y+4))^bx+(5y+3x-6)dy=0其中 L 为三顶点分别为 ( 0 , 0 ) , ( 4 , 0 ) 和 ( 4 , 2 ) 的三角形的正向边界 A 2 B 4 C 8 D 16
计算曲线积分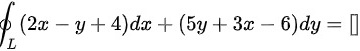
其中 L 为三顶点分别为 ( 0 , 0 ) , ( 4 , 0 ) 和 ( 4 , 2 ) 的三角形的正向边界
A 2
B 4
C 8
D 16
题目解答
答案
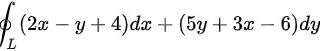
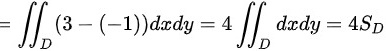
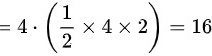
故答案选D，其余选项均不正确。
解析
步骤 1：应用格林公式
格林公式是用于计算平面区域上曲线积分的一种方法。对于一个闭合曲线L，如果L围成的区域D内函数P(x,y)和Q(x,y)具有连续的一阶偏导数，那么有
$$\oint_{L} P(x,y)dx + Q(x,y)dy = \iint_{D} \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dxdy$$
其中，P(x,y) = 2x - y + 4，Q(x,y) = 5y + 3x - 6。
步骤 2：计算偏导数
计算P(x,y)和Q(x,y)的偏导数：
$$\frac{\partial Q}{\partial x} = 3$$
$$\frac{\partial P}{\partial y} = -1$$
因此，$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 3 - (-1) = 4$。
步骤 3：计算二重积分
根据格林公式，原曲线积分可以转化为二重积分：
$$\oint_{L} (2x-y+4)dx + (5y+3x-6)dy = \iint_{D} 4 dxdy$$
其中，D是三角形区域，其面积为$S_D = \frac{1}{2} \times 4 \times 2 = 4$。
因此，$\iint_{D} 4 dxdy = 4 \times S_D = 4 \times 4 = 16$。
格林公式是用于计算平面区域上曲线积分的一种方法。对于一个闭合曲线L，如果L围成的区域D内函数P(x,y)和Q(x,y)具有连续的一阶偏导数，那么有
$$\oint_{L} P(x,y)dx + Q(x,y)dy = \iint_{D} \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dxdy$$
其中，P(x,y) = 2x - y + 4，Q(x,y) = 5y + 3x - 6。
步骤 2：计算偏导数
计算P(x,y)和Q(x,y)的偏导数：
$$\frac{\partial Q}{\partial x} = 3$$
$$\frac{\partial P}{\partial y} = -1$$
因此，$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 3 - (-1) = 4$。
步骤 3：计算二重积分
根据格林公式，原曲线积分可以转化为二重积分：
$$\oint_{L} (2x-y+4)dx + (5y+3x-6)dy = \iint_{D} 4 dxdy$$
其中，D是三角形区域，其面积为$S_D = \frac{1}{2} \times 4 \times 2 = 4$。
因此，$\iint_{D} 4 dxdy = 4 \times S_D = 4 \times 4 = 16$。