设随机变量 sim U(a,b) ,求D(X).
题目解答
答案
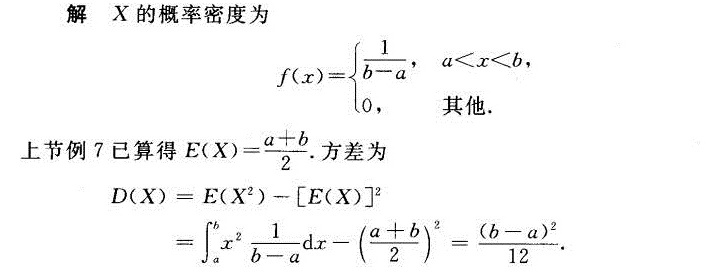
解析
考查要点:本题主要考查均匀分布(连续型)的方差计算,需要掌握方差的定义以及均匀分布的概率密度函数。
解题核心思路:
- 方差公式:$D(X) = E(X^2) - [E(X)]^2$,其中$E(X)$已知为$\dfrac{a+b}{2}$。
- 计算$E(X^2)$:利用均匀分布的概率密度函数,通过积分求解。
- 代数化简:将积分结果与$[E(X)]^2$相减,最终化简得到方差表达式。
破题关键点:
- 积分计算:正确计算$\int_a^b x^2 \cdot \dfrac{1}{b-a} dx$。
- 代数技巧:将结果化简为$(b-a)^2/12$的形式。
步骤1:计算$E(X^2)$
根据期望的定义:
$E(X^2) = \int_{-\infty}^{+\infty} x^2 f(x) dx = \int_a^b x^2 \cdot \dfrac{1}{b-a} dx$
计算积分:
$\int_a^b x^2 dx = \left[ \dfrac{x^3}{3} \right]_a^b = \dfrac{b^3 - a^3}{3}$
因此:
$E(X^2) = \dfrac{1}{b-a} \cdot \dfrac{b^3 - a^3}{3} = \dfrac{b^3 - a^3}{3(b-a)}$
利用立方差公式$b^3 - a^3 = (b-a)(b^2 + ab + a^2)$,化简得:
$E(X^2) = \dfrac{b^2 + ab + a^2}{3}$
步骤2:计算$[E(X)]^2$
已知$E(X) = \dfrac{a+b}{2}$,因此:
$[E(X)]^2 = \left( \dfrac{a+b}{2} \right)^2 = \dfrac{a^2 + 2ab + b^2}{4}$
步骤3:计算方差$D(X)$
根据方差公式:
$D(X) = E(X^2) - [E(X)]^2 = \dfrac{a^2 + ab + b^2}{3} - \dfrac{a^2 + 2ab + b^2}{4}$
通分后:
$D(X) = \dfrac{4(a^2 + ab + b^2) - 3(a^2 + 2ab + b^2)}{12} = \dfrac{(4a^2 - 3a^2) + (4ab - 6ab) + (4b^2 - 3b^2)}{12}$
化简分子:
$D(X) = \dfrac{a^2 - 2ab + b^2}{12} = \dfrac{(b - a)^2}{12}$