题目

3. 设随机变量 X 的密度函数为 , 则 Y=3-2 X 的密度函数为 ( ) .(A) (B) (C) (D)

3. 设随机变量 X 的密度函数为 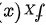$f_X(x)$ , 则 Y=3-2 X 的密度函数为 ( ) .

(A) 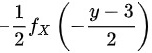$-\frac{1}{2}f_X\left(-\frac{y-3}{2}\right)$

(B) 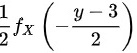$\frac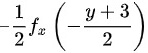{1}{2}f_X\left(-\frac{y-3}{2}\right)$

(D) 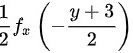$\frac{1}{2}f_x\left(-\frac{y+3}{2}\right)$

题目解答

答案

根据题意，随机变量X的密度函数为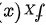 $f_X(x)$ ，Y=3 - 2X。

设 Z = g(X) = 3 - 2X，则有：

$g^{-1}(y)=\frac{3-y}{2}$

$\left|\frac{d}{dy}g^{-1}(y)\right|=\frac{1}{2}$

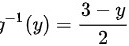
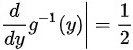
根据变量代换法的公式，我们有：

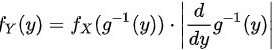
$f_Y(y)=f_X(g^{-1}(y))\cdot\left|\frac{d}{dy}g^{-1}(y)\right|$

代入上面的公式，我们有：

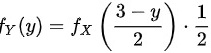
$f_Y(y)=f_X\left(\frac{3-y}{2}\right)\cdot\frac{1}{2}$

因此，正确答案为 B，即 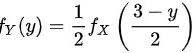$f_Y(y)=\frac{1}{2}f_X\left(\frac{3-y}{2}\right)$ 。

综上所述，本题的答案为 B。

解析

步骤 1：定义变量代换
设 $Z = g(X) = 3 - 2X$，则有 $X = g^{-1}(Y) = \dfrac{3 - Y}{2}$。
步骤 2：计算导数
计算 $g^{-1}(Y)$ 的导数，即 $\dfrac{d}{dy}g^{-1}(y) = \dfrac{d}{dy}\left(\dfrac{3 - y}{2}\right) = -\dfrac{1}{2}$。
步骤 3：应用变量代换公式
根据变量代换法的公式，我们有 $f_Y(y) = f_X(g^{-1}(y)) \cdot \left|\dfrac{d}{dy}g^{-1}(y)\right|$。
代入上面的公式，我们有 $f_Y(y) = f_X\left(\dfrac{3 - y}{2}\right) \cdot \left|-\dfrac{1}{2}\right| = \dfrac{1}{2}f_X\left(\dfrac{3 - y}{2}\right)$。