题目
设_(1)=iint ((x)^3+(y)^3)de，_(1)=iint ((x)^3+(y)^3)de，_(1)=iint ((x)^3+(y)^3)de，其中_(1)=iint ((x)^3+(y)^3)de为单位圆域_(1)=iint ((x)^3+(y)^3)de，则二重积分的大小顺序为（）A._(1)=iint ((x)^3+(y)^3)deB._(1)=iint ((x)^3+(y)^3)deC._(1)=iint ((x)^3+(y)^3)deD._(1)=iint ((x)^3+(y)^3)de
设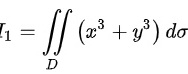
，
，
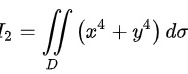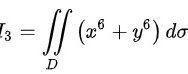，其中
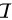为单位圆域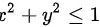
，则二重积分的大小顺序为（）
A.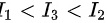
B.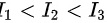
C.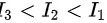
D.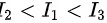
题目解答
答案
在单位圆域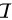内任取一点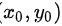
∵
∴
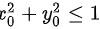
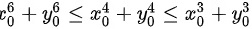
该不等式对单位圆域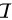内的所有点都成立，且只有在
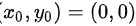时该不等式取等号，
∴题干中三个二重积分的大小顺序为
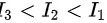
正确答案为选项C
解析
步骤 1：确定单位圆域内的点
在单位圆域D内任取一点(x0,y0)，满足${{x}_{0}}^{2}+{{y}_{0}}^{2}\leqslant 1$。
步骤 2：比较不同幂次的表达式
由于${{x}_{0}}^{2}+{{y}_{0}}^{2}\leqslant 1$，可以推导出${{x}_{0}}^{6}+{{y}_{0}}^{6}\leqslant {{x}_{0}}^{4}+{{y}_{0}}^{4}\leqslant {{x}_{0}}^{2}+{{y}_{0}}^{2}$。这是因为幂次越高，当x和y的绝对值小于1时，其值越小。
步骤 3：确定二重积分的大小顺序
由于上述不等式对单位圆域D内的所有点都成立，且只有在$({x}_{0},{y}_{0})=(0,0)$时该不等式取等号，因此可以确定二重积分的大小顺序为${I}_{3}\lt {I}_{2}\lt {I}_{1}$。
在单位圆域D内任取一点(x0,y0)，满足${{x}_{0}}^{2}+{{y}_{0}}^{2}\leqslant 1$。
步骤 2：比较不同幂次的表达式
由于${{x}_{0}}^{2}+{{y}_{0}}^{2}\leqslant 1$，可以推导出${{x}_{0}}^{6}+{{y}_{0}}^{6}\leqslant {{x}_{0}}^{4}+{{y}_{0}}^{4}\leqslant {{x}_{0}}^{2}+{{y}_{0}}^{2}$。这是因为幂次越高，当x和y的绝对值小于1时，其值越小。
步骤 3：确定二重积分的大小顺序
由于上述不等式对单位圆域D内的所有点都成立，且只有在$({x}_{0},{y}_{0})=(0,0)$时该不等式取等号，因此可以确定二重积分的大小顺序为${I}_{3}\lt {I}_{2}\lt {I}_{1}$。