题目
)(本题满分10分)-|||-求函数 (x,y)=(x)^3+8(y)^3-xy 的极值.
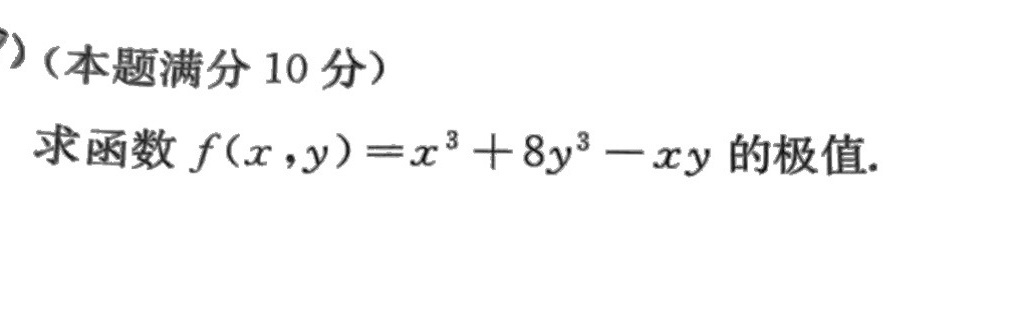
题目解答
答案

解析
步骤 1:求偏导数
首先,我们需要计算函数 $f(x,y)={x}^{3}+8{y}^{3}-xy$ 的偏导数。对于 $x$ 的偏导数,我们得到 $f_x=3{x}^{2}-y$;对于 $y$ 的偏导数,我们得到 $f_y=24{y}^{2}-x$。
步骤 2:求驻点
接下来,我们需要找到函数的驻点,即偏导数同时为零的点。因此,我们需要解方程组:
$$
\begin{cases}
3{x}^{2}-y=0 \\
24{y}^{2}-x=0
\end{cases}
$$
从第一个方程中,我们得到 $y=3{x}^{2}$。将这个表达式代入第二个方程中,我们得到 $24(3{x}^{2})^{2}-x=0$,即 $216{x}^{4}-x=0$。解这个方程,我们得到 $x=0$ 或 $x=\dfrac {1}{6}$。当 $x=0$ 时,$y=0$;当 $x=\dfrac {1}{6}$ 时,$y=\dfrac {1}{12}$。因此,我们得到两个驻点 $(0,0)$ 和 $(\dfrac {1}{6},\dfrac {1}{12})$。
步骤 3:判断极值
为了判断这些驻点是否为极值点,我们需要计算二阶偏导数。对于 $x$ 的二阶偏导数,我们得到 $f_{xx}=6x$;对于 $y$ 的二阶偏导数,我们得到 $f_{yy}=48y$;对于 $x$ 和 $y$ 的混合偏导数,我们得到 $f_{xy}=-1$。然后,我们需要计算判别式 $D=f_{xx}f_{yy}-(f_{xy})^{2}$。对于驻点 $(0,0)$,我们得到 $D=0$,因此无法判断该点是否为极值点。对于驻点 $(\dfrac {1}{6},\dfrac {1}{12})$,我们得到 $D=6(\dfrac {1}{6})\cdot48(\dfrac {1}{12})-(-1)^{2}=4-1=3>0$,且 $f_{xx}=6(\dfrac {1}{6})=1>0$,因此该点为极小值点。
首先,我们需要计算函数 $f(x,y)={x}^{3}+8{y}^{3}-xy$ 的偏导数。对于 $x$ 的偏导数,我们得到 $f_x=3{x}^{2}-y$;对于 $y$ 的偏导数,我们得到 $f_y=24{y}^{2}-x$。
步骤 2:求驻点
接下来,我们需要找到函数的驻点,即偏导数同时为零的点。因此,我们需要解方程组:
$$
\begin{cases}
3{x}^{2}-y=0 \\
24{y}^{2}-x=0
\end{cases}
$$
从第一个方程中,我们得到 $y=3{x}^{2}$。将这个表达式代入第二个方程中,我们得到 $24(3{x}^{2})^{2}-x=0$,即 $216{x}^{4}-x=0$。解这个方程,我们得到 $x=0$ 或 $x=\dfrac {1}{6}$。当 $x=0$ 时,$y=0$;当 $x=\dfrac {1}{6}$ 时,$y=\dfrac {1}{12}$。因此,我们得到两个驻点 $(0,0)$ 和 $(\dfrac {1}{6},\dfrac {1}{12})$。
步骤 3:判断极值
为了判断这些驻点是否为极值点,我们需要计算二阶偏导数。对于 $x$ 的二阶偏导数,我们得到 $f_{xx}=6x$;对于 $y$ 的二阶偏导数,我们得到 $f_{yy}=48y$;对于 $x$ 和 $y$ 的混合偏导数,我们得到 $f_{xy}=-1$。然后,我们需要计算判别式 $D=f_{xx}f_{yy}-(f_{xy})^{2}$。对于驻点 $(0,0)$,我们得到 $D=0$,因此无法判断该点是否为极值点。对于驻点 $(\dfrac {1}{6},\dfrac {1}{12})$,我们得到 $D=6(\dfrac {1}{6})\cdot48(\dfrac {1}{12})-(-1)^{2}=4-1=3>0$,且 $f_{xx}=6(\dfrac {1}{6})=1>0$,因此该点为极小值点。