题目
6. (f(x)在 _{0)=(x)_(0) 处可导,且 lim _(harrow 0)dfrac (f({x)_(0)+2h)-f((x)_(0)-h)}(2h)= () .-|||-A. dfrac (3)(2)f((x)_(0)) B -dfrac (2)(3)f((x)_(0)) C. dfrac (3)(2)f'((x)_(0)) D. -dfrac (3)(2)f'((x)_(0))-|||-7.设 (x)=arctan (e)^x, 则 '= ()
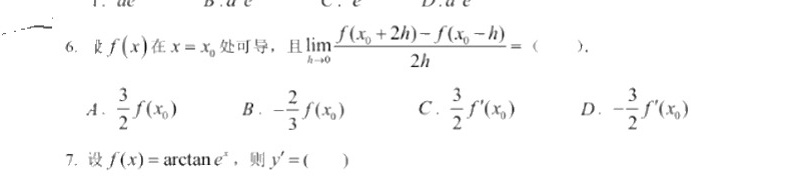
题目解答
答案

解析
步骤 1:将给定的极限表达式拆分为两个部分
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0}-h)}{2h} = \lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0})}{2h} + \lim _{h\rightarrow 0}\dfrac {f({x}_{0})-f({x}_{0}-h)}{2h}$
步骤 2:利用导数的定义
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0})}{2h} = f'({x}_{0})$,$\lim _{h\rightarrow 0}\dfrac {f({x}_{0})-f({x}_{0}-h)}{2h} = \dfrac{1}{2}f'({x}_{0})$
步骤 3:将两部分相加
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0}-h)}{2h} = f'({x}_{0}) + \dfrac{1}{2}f'({x}_{0}) = \dfrac{3}{2}f'({x}_{0})$
【答案】
C. $\dfrac {3}{2}f'({x}_{0})$
7.设 $f(x)=\arctan {e}^{x}$ ,则 y'= ()
【解析】
步骤 1:使用链式法则
$f'(x) = \dfrac{d}{dx}(\arctan {e}^{x}) = \dfrac{1}{1+({e}^{x})^2} \cdot \dfrac{d}{dx}({e}^{x})$
步骤 2:计算导数
$f'(x) = \dfrac{1}{1+{e}^{2x}} \cdot {e}^{x} = \dfrac{{e}^{x}}{1+{e}^{2x}}$
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0}-h)}{2h} = \lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0})}{2h} + \lim _{h\rightarrow 0}\dfrac {f({x}_{0})-f({x}_{0}-h)}{2h}$
步骤 2:利用导数的定义
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0})}{2h} = f'({x}_{0})$,$\lim _{h\rightarrow 0}\dfrac {f({x}_{0})-f({x}_{0}-h)}{2h} = \dfrac{1}{2}f'({x}_{0})$
步骤 3:将两部分相加
$\lim _{h\rightarrow 0}\dfrac {f({x}_{0}+2h)-f({x}_{0}-h)}{2h} = f'({x}_{0}) + \dfrac{1}{2}f'({x}_{0}) = \dfrac{3}{2}f'({x}_{0})$
【答案】
C. $\dfrac {3}{2}f'({x}_{0})$
7.设 $f(x)=\arctan {e}^{x}$ ,则 y'= ()
【解析】
步骤 1:使用链式法则
$f'(x) = \dfrac{d}{dx}(\arctan {e}^{x}) = \dfrac{1}{1+({e}^{x})^2} \cdot \dfrac{d}{dx}({e}^{x})$
步骤 2:计算导数
$f'(x) = \dfrac{1}{1+{e}^{2x}} \cdot {e}^{x} = \dfrac{{e}^{x}}{1+{e}^{2x}}$