题目
函数=3(x)^2-5 -5在定义域上可取得()A.最大值-5B.最大值5C.最小值-5D.最小值5
函数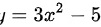
-5在定义域上可取得()
A.最大值-5
B.最大值5
C.最小值-5
D.最小值5
题目解答
答案
解：由题可得
二次函数的最大值为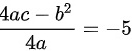
又因为函数的开口向上，所以存在最小值
故选C
解析
步骤 1：确定函数类型
函数$y=3{x}^{2}-5$是一个二次函数，其一般形式为$y=ax^2+bx+c$，其中$a=3$，$b=0$，$c=-5$。
步骤 2：分析二次函数的开口方向
由于$a=3>0$，所以函数的开口方向向上，这意味着函数有最小值，而没有最大值。
步骤 3：计算二次函数的最小值
二次函数的最小值可以通过顶点公式计算，顶点的横坐标$x=-\frac{b}{2a}$，代入$a=3$，$b=0$，得到$x=0$。将$x=0$代入原函数$y=3{x}^{2}-5$，得到$y=3(0)^2-5=-5$。因此，函数的最小值为-5。
函数$y=3{x}^{2}-5$是一个二次函数，其一般形式为$y=ax^2+bx+c$，其中$a=3$，$b=0$，$c=-5$。
步骤 2：分析二次函数的开口方向
由于$a=3>0$，所以函数的开口方向向上，这意味着函数有最小值，而没有最大值。
步骤 3：计算二次函数的最小值
二次函数的最小值可以通过顶点公式计算，顶点的横坐标$x=-\frac{b}{2a}$，代入$a=3$，$b=0$，得到$x=0$。将$x=0$代入原函数$y=3{x}^{2}-5$，得到$y=3(0)^2-5=-5$。因此，函数的最小值为-5。