题目
将函数(x)=dfrac (1)({x)^2+x}展开成(x)=dfrac (1)({x)^2+x} 的幂级数,并写出可展区间
将函数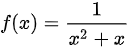 展开成
展开成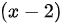 的幂级数,并写出可展区间
的幂级数,并写出可展区间
题目解答
答案
依题意,得
函数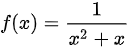
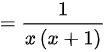
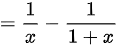
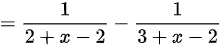
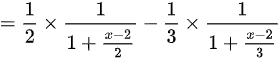
根据泰勒级数展开式,知:
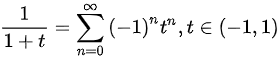
∴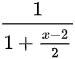
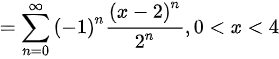
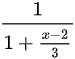
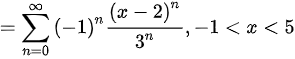
∴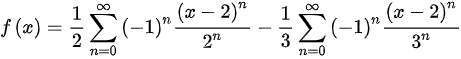
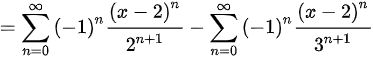
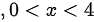
解析
步骤 1:函数分解
将函数$f(x)=\dfrac {1}{{x}^{2}+x}$分解为两个部分,以便于后续的幂级数展开。
$f(x)=\dfrac {1}{x(x+1)}=\dfrac {1}{x}-\dfrac {1}{1+x}$
步骤 2:变量替换
将函数中的$x$替换为$x-2$,以便于将函数展开为$(x-2)$的幂级数。
$f(x)=\dfrac {1}{2+x-2}-\dfrac {1}{3+x-2}$
$=\dfrac {1}{2}\times \dfrac {1}{1+\dfrac {x-2}{2}}-\dfrac {1}{3}\times \dfrac {1}{1+\dfrac {x-2}{3}}$
步骤 3:幂级数展开
利用泰勒级数展开式,将函数展开为$(x-2)$的幂级数。
$\dfrac {1}{1+t}=\sum _{n=0}^{\infty }{(-1)}^{n}{t}^{n}$,其中$t\in (-1,1)$
$\dfrac {1}{1+\dfrac {x-2}{2}}=\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{2}^{n}}$,其中$0\lt x\lt 4$
$\dfrac {1}{1+\dfrac {x-2}{3}}=\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{3}^{n}}$,其中$-1\lt x\lt 5$
步骤 4:合并幂级数
将两个幂级数合并,得到$f(x)$的幂级数展开式。
$f(x)=\dfrac {1}{2}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{2}^{n}}-\dfrac {1}{3}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{3}^{n}}$
$=\sum _{n=0}^{\infty }{(-1)}^{n}\left(\dfrac {1}{2^{n+1}}-\dfrac {1}{3^{n+1}}\right)(x-2)^{n}$
步骤 5:确定可展区间
根据幂级数的收敛条件,确定函数$f(x)$的可展区间。
由于幂级数的收敛条件为$0\lt x\lt 4$和$-1\lt x\lt 5$,因此函数$f(x)$的可展区间为$0\lt x\lt 4$。
将函数$f(x)=\dfrac {1}{{x}^{2}+x}$分解为两个部分,以便于后续的幂级数展开。
$f(x)=\dfrac {1}{x(x+1)}=\dfrac {1}{x}-\dfrac {1}{1+x}$
步骤 2:变量替换
将函数中的$x$替换为$x-2$,以便于将函数展开为$(x-2)$的幂级数。
$f(x)=\dfrac {1}{2+x-2}-\dfrac {1}{3+x-2}$
$=\dfrac {1}{2}\times \dfrac {1}{1+\dfrac {x-2}{2}}-\dfrac {1}{3}\times \dfrac {1}{1+\dfrac {x-2}{3}}$
步骤 3:幂级数展开
利用泰勒级数展开式,将函数展开为$(x-2)$的幂级数。
$\dfrac {1}{1+t}=\sum _{n=0}^{\infty }{(-1)}^{n}{t}^{n}$,其中$t\in (-1,1)$
$\dfrac {1}{1+\dfrac {x-2}{2}}=\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{2}^{n}}$,其中$0\lt x\lt 4$
$\dfrac {1}{1+\dfrac {x-2}{3}}=\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{3}^{n}}$,其中$-1\lt x\lt 5$
步骤 4:合并幂级数
将两个幂级数合并,得到$f(x)$的幂级数展开式。
$f(x)=\dfrac {1}{2}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{2}^{n}}-\dfrac {1}{3}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-2)}^{n}}{{3}^{n}}$
$=\sum _{n=0}^{\infty }{(-1)}^{n}\left(\dfrac {1}{2^{n+1}}-\dfrac {1}{3^{n+1}}\right)(x-2)^{n}$
步骤 5:确定可展区间
根据幂级数的收敛条件,确定函数$f(x)$的可展区间。
由于幂级数的收敛条件为$0\lt x\lt 4$和$-1\lt x\lt 5$,因此函数$f(x)$的可展区间为$0\lt x\lt 4$。