题目
设=y(x)由参数=y(x)所确定的隐函数,求=y(x).
设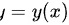 由参数
由参数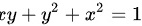 所确定的隐函数,求
所确定的隐函数,求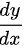 .
.
题目解答
答案
解:已知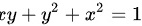 ,
,
使等式两边同时对 求导,得:
求导,得:
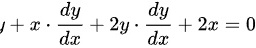 ,
,
化简整理得: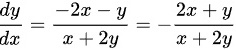 ,
,
所以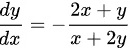 .
.
解析
考查要点:本题主要考查隐函数求导法的应用,需要掌握乘积法则和链式法则,并能正确分离变量求出导数表达式。
解题核心思路:
- 对等式两边同时关于$x$求导,注意将$y$视为$x$的函数,使用链式法则处理含$y$的项。
- 整理含有$\dfrac{dy}{dx}$的项,将其余项移到等式另一边。
- 最终解出$\dfrac{dy}{dx}$的表达式。
破题关键点:
- 正确应用乘积法则对$xy$项求导。
- 链式法则处理$y^2$项的导数。
- 代数整理时注意符号和因式分解。
已知方程:
$xy + y^2 + x^2 = 1$
步骤1:对等式两边同时关于$x$求导
- $xy$项:应用乘积法则,导数为$y + x\dfrac{dy}{dx}$。
- $y^2$项:应用链式法则,导数为$2y \cdot \dfrac{dy}{dx}$。
- $x^2$项:导数为$2x$。
- 右边常数项:导数为$0$。
整理得:
$y + x\dfrac{dy}{dx} + 2y\dfrac{dy}{dx} + 2x = 0$
步骤2:分离$\dfrac{dy}{dx}$项
将含$\dfrac{dy}{dx}$的项合并:
$(x + 2y)\dfrac{dy}{dx} = - (y + 2x)$
步骤3:解出$\dfrac{dy}{dx}$
两边同除以$(x + 2y)$:
$\dfrac{dy}{dx} = -\dfrac{y + 2x}{x + 2y} = -\dfrac{2x + y}{x + 2y}$