题目
设 f ( x ) 连续且(int )_(0)^xf(t)dt=1+(x)^3 则 f ( 1 ) = a 3 b 2 c 0 d 9
设 f ( x ) 连续且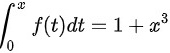
则 f ( 1 ) =
a 3
b 2
c 0
d 9
题目解答
答案
∵
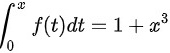
两边同时求导数微分符号
∵
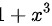代入求导公式得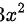
根据积分求导公式: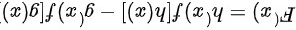
∵
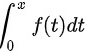求导为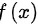 
∴
将x=1代入
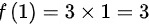
所以答案选a 3
解析
步骤 1：求导数
对等式${\int }_{0}^{x}f(t)dt=1+{x}^{3}$两边同时求导，根据微积分基本定理，左边的导数为$f(x)$，右边的导数为$3x^2$。
步骤 2：求$f(x)$
根据步骤1，我们得到$f(x)=3x^2$。
步骤 3：求$f(1)$
将$x=1$代入$f(x)=3x^2$，得到$f(1)=3\times 1^2=3$。
对等式${\int }_{0}^{x}f(t)dt=1+{x}^{3}$两边同时求导，根据微积分基本定理，左边的导数为$f(x)$，右边的导数为$3x^2$。
步骤 2：求$f(x)$
根据步骤1，我们得到$f(x)=3x^2$。
步骤 3：求$f(1)$
将$x=1$代入$f(x)=3x^2$，得到$f(1)=3\times 1^2=3$。