题目
求函数(x,y)=(e)^2x(x+(y)^2+2y) 的极值。
求函数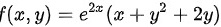 的极值。
的极值。
题目解答
答案
对于二元函数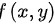 ,求极值的步骤为:
,求极值的步骤为:
(1)求函数的驻点(即满足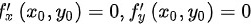 的点);
的点);
(2)利用极值充分条件:
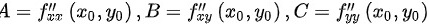
若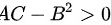 0" data-width="116" data-height="25" data-size="1599" data-format="png" style="max-width:100%">,
0" data-width="116" data-height="25" data-size="1599" data-format="png" style="max-width:100%">,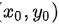 为极值点:A<0,为极大值点;A>0,为极小值点。若
为极值点:A<0,为极大值点;A>0,为极小值点。若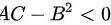 ,
,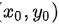 不为极值点。由此判定驻点是否为极值点。
不为极值点。由此判定驻点是否为极值点。
本题函数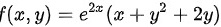
求一阶偏导数:
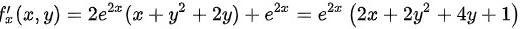
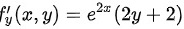
令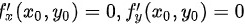 ,可得驻点:
,可得驻点: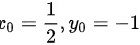 .
.
继续求二阶偏导数:
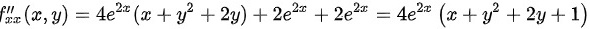
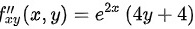
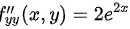
可得: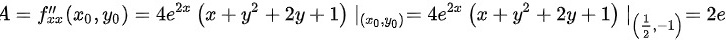
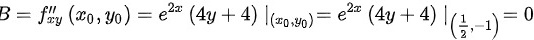
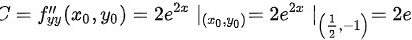
由极值充分条件进行判断求解: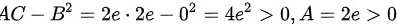 0,A=2e>0" data-width="402" data-height="26" data-size="4480" data-format="png" style="max-width:100%">
0,A=2e>0" data-width="402" data-height="26" data-size="4480" data-format="png" style="max-width:100%">
故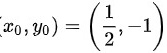 为极小值点,极小值为
为极小值点,极小值为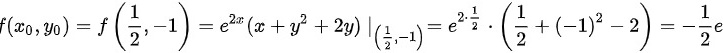
故函数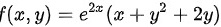 的极小值为
的极小值为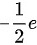 .
.
解析
考查要点:本题主要考查二元函数极值的求解方法,包括驻点的求解、二阶偏导数的计算以及极值的充分条件判断。
解题核心思路:
- 求驻点:通过求一阶偏导数并解方程组,找到可能的极值点。
- 二阶偏导数计算:计算二阶偏导数,构建判别式$AC - B^2$。
- 极值判断:根据判别式的结果及$A$的符号,确定驻点是否为极值点及其类型。
破题关键点:
- 正确求解一阶偏导数,特别注意乘积法则的应用。
- 代入驻点计算二阶偏导数时,需准确代入坐标值。
- 判别式的符号分析是判断极值类型的核心。
求驻点
-
计算一阶偏导数:
- 对$x$求偏导:
$f_x = \frac{\partial}{\partial x} \left( e^{2x}(x + y^2 + 2y) \right) = e^{2x}(2x + 2y^2 + 4y + 1)$ - 对$y$求偏导:
$f_y = \frac{\partial}{\partial y} \left( e^{2x}(x + y^2 + 2y) \right) = e^{2x}(2y + 2)$
- 对$x$求偏导:
-
解方程组:
- 令$f_y = 0$,得$2y + 2 = 0 \Rightarrow y = -1$。
- 代入$f_x = 0$,得:
$e^{2x}(2x + 2(-1)^2 + 4(-1) + 1) = 0 \Rightarrow 2x - 1 = 0 \Rightarrow x = \frac{1}{2}$ - 驻点为$\left( \frac{1}{2}, -1 \right)$。
二阶偏导数与极值判断
-
计算二阶偏导数:
- $f_{xx} = \frac{\partial}{\partial x} \left( e^{2x}(2x + 2y^2 + 4y + 1) \right) = e^{2x}(4x + 4y^2 + 8y + 4)$
- $f_{xy} = \frac{\partial}{\partial y} \left( e^{2x}(2x + 2y^2 + 4y + 1) \right) = e^{2x}(4y + 4)$
- $f_{yy} = \frac{\partial}{\partial y} \left( e^{2x}(2y + 2) \right) = 2e^{2x}$
-
代入驻点:
- $A = f_{xx}\left( \frac{1}{2}, -1 \right) = 2e$
- $B = f_{xy}\left( \frac{1}{2}, -1 \right) = 0$
- $C = f_{yy}\left( \frac{1}{2}, -1 \right) = 2e$
-
判别式:
$AC - B^2 = (2e)(2e) - 0^2 = 4e^2 > 0, \quad A = 2e > 0$
因此,$\left( \frac{1}{2}, -1 \right)$为极小值点。
计算极小值
$f\left( \frac{1}{2}, -1 \right) = e^{2 \cdot \frac{1}{2}} \left( \frac{1}{2} + (-1)^2 + 2(-1) \right) = e \cdot \left( -\frac{1}{2} \right) = -\frac{1}{2}e$