题目
58.点 (-2,-1) 在圆 ((x-1))^2+((y+1))^2=8 内.( )
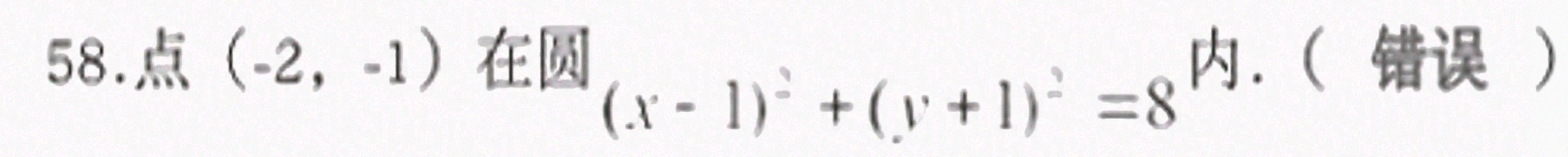
题目解答
答案
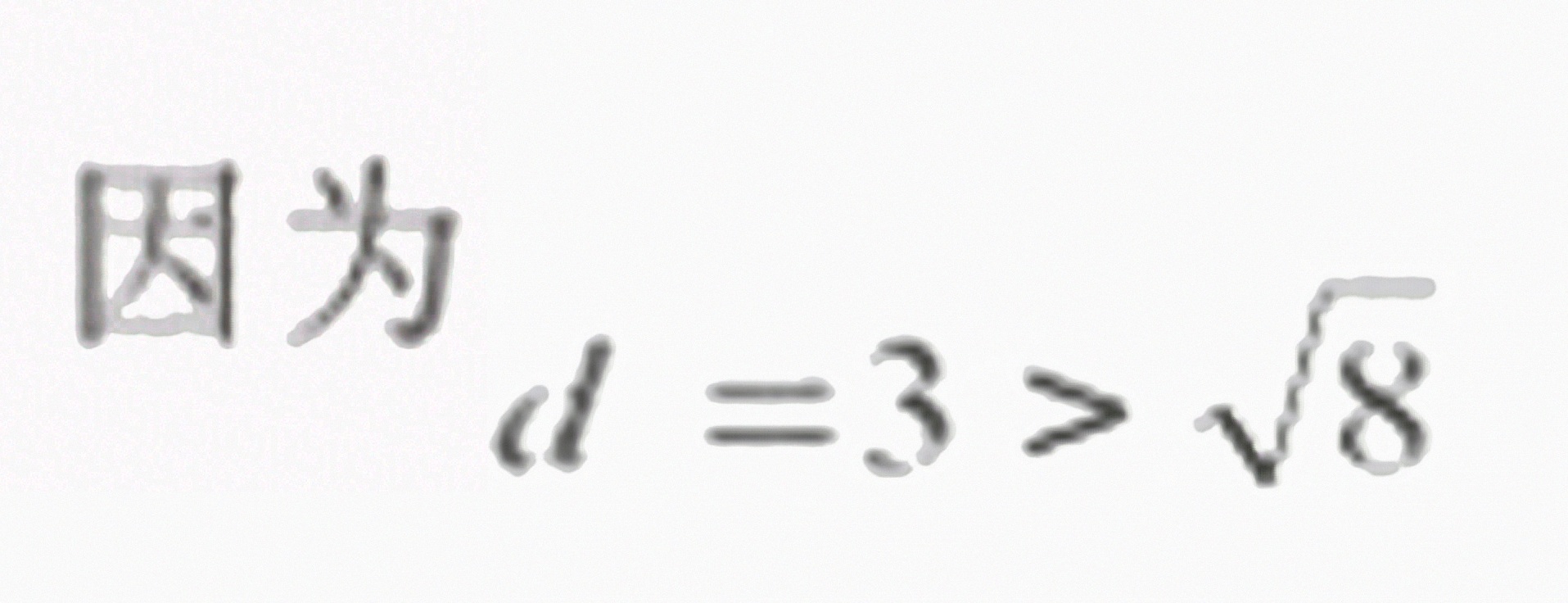
解析
考查要点:判断点与圆的位置关系。
解题思路:
- 确定圆心和半径:根据圆的标准方程 $(x-h)^2 + (y-k)^2 = r^2$,直接读出圆心 $(h,k)$ 和半径 $r$。
- 计算点到圆心的距离:利用两点间距离公式,计算已知点到圆心的距离。
- 比较距离与半径:若距离平方小于半径平方,则点在圆内;等于则在圆上;大于则在圆外。
步骤1:确定圆心和半径
圆的标准方程为 $(x-1)^2 + (y+1)^2 = 8$,因此:
- 圆心为 $(1, -1)$
- 半径平方为 $8$,即 $r = \sqrt{8} = 2\sqrt{2}$
步骤2:计算点到圆心的距离平方
已知点 $(-2, -1)$,圆心 $(1, -1)$,距离平方为:
$\begin{aligned} d^2 &= (-2 - 1)^2 + (-1 - (-1))^2 \\ &= (-3)^2 + 0^2 \\ &= 9 + 0 \\ &= 9 \end{aligned}$
步骤3:比较距离平方与半径平方
- $d^2 = 9$,$r^2 = 8$
- 因为 $9 > 8$,所以点 $(-2, -1)$ 在圆外。
结论:题目中“点在圆内”的说法错误。