题目
设四元非齐次线性方程组的系数矩阵的秩为 ,已知 是它的 个解向量,且 ,,,求该方程组的通解 .
设四元非齐次线性方程组的系数矩阵的秩为 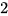 ,已知
,已知 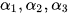 是它的
是它的 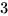 个解向量,且
个解向量,且 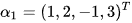 ,
, ,
,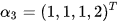 ,求该方程组的通解 .
,求该方程组的通解 .
题目解答
答案
设该非齐次线性方程组的系数矩阵为 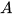 ,增广矩阵为
,增广矩阵为 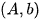
 四元非齐次线性方程组的系数矩阵的秩为
四元非齐次线性方程组的系数矩阵的秩为 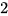
 对应
对应 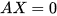 的基础解系所含解向量的个数为
的基础解系所含解向量的个数为 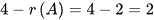

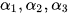 是
是 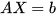 的
的 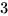 个解向量
个解向量
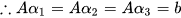
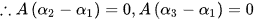
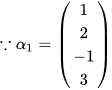 ,
, ,
,
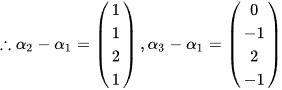 是
是 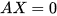 的基础解系
的基础解系
 该方程组的通解为
该方程组的通解为 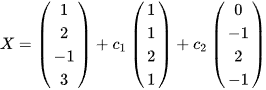 ,其中
,其中 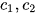 为任意常数
为任意常数
解析
步骤 1:确定基础解系的个数
四元非齐次线性方程组的系数矩阵的秩为2,因此,对应齐次线性方程组的基础解系所含解向量的个数为4-2=2。
步骤 2:确定非齐次线性方程组的特解
已知α1,α2,α3是该非齐次线性方程组的解向量,因此,α1可以作为非齐次线性方程组的一个特解。
步骤 3:确定齐次线性方程组的基础解系
由于α1,α2,α3是该非齐次线性方程组的解向量,因此,α2-α1和α3-α1是对应齐次线性方程组的解向量。计算这两个向量:
${\alpha }_{2}-{\alpha }_{1}={(2,3,1,4)}^{T}-{(1,2,-1,3)}^{T}={(1,1,2,1)}^{T}$
${\alpha }_{3}-{\alpha }_{1}={(1,1,1,2)}^{T}-{(1,2,-1,3)}^{T}={(0,-1,2,-1)}^{T}$
这两个向量线性无关,因此,它们可以作为齐次线性方程组的基础解系。
步骤 4:写出非齐次线性方程组的通解
非齐次线性方程组的通解为特解加上齐次线性方程组的通解,即:
$X={\alpha }_{1}+{c}_{1}({\alpha }_{2}-{\alpha }_{1})+{c}_{2}({\alpha }_{3}-{\alpha }_{1})$
其中,c1和c2为任意常数。
四元非齐次线性方程组的系数矩阵的秩为2,因此,对应齐次线性方程组的基础解系所含解向量的个数为4-2=2。
步骤 2:确定非齐次线性方程组的特解
已知α1,α2,α3是该非齐次线性方程组的解向量,因此,α1可以作为非齐次线性方程组的一个特解。
步骤 3:确定齐次线性方程组的基础解系
由于α1,α2,α3是该非齐次线性方程组的解向量,因此,α2-α1和α3-α1是对应齐次线性方程组的解向量。计算这两个向量:
${\alpha }_{2}-{\alpha }_{1}={(2,3,1,4)}^{T}-{(1,2,-1,3)}^{T}={(1,1,2,1)}^{T}$
${\alpha }_{3}-{\alpha }_{1}={(1,1,1,2)}^{T}-{(1,2,-1,3)}^{T}={(0,-1,2,-1)}^{T}$
这两个向量线性无关,因此,它们可以作为齐次线性方程组的基础解系。
步骤 4:写出非齐次线性方程组的通解
非齐次线性方程组的通解为特解加上齐次线性方程组的通解,即:
$X={\alpha }_{1}+{c}_{1}({\alpha }_{2}-{\alpha }_{1})+{c}_{2}({\alpha }_{3}-{\alpha }_{1})$
其中,c1和c2为任意常数。