题目
4.设离散型随机变量X的分布函数为 F(x)= 0, x
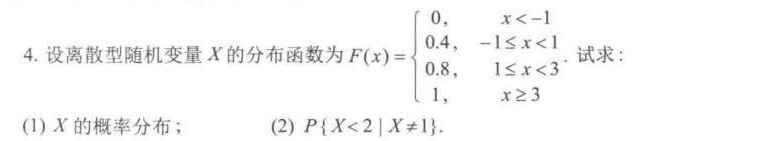
题目解答
答案

解析
步骤 1:求X的概率分布
根据分布函数F(x)的定义,我们可以求出X取不同值的概率。对于离散型随机变量,分布函数F(x)在每个跳跃点处的跳跃值即为该点的概率。
- 当 $x=-1$ 时,$F(-1)=0.4$,所以 $P(X=-1)=0.4$。
- 当 $x=1$ 时,$F(1)=0.8$,所以 $P(X=1)=F(1)-F(-1)=0.8-0.4=0.4$。
- 当 $x=3$ 时,$F(3)=1$,所以 $P(X=3)=F(3)-F(1)=1-0.8=0.2$。
步骤 2:求 $P\{ X\lt 2|X\neq 1\} $
根据条件概率的定义,$P\{ X\lt 2|X\neq 1\} =\frac{P\{ X\lt 2\cap X\neq 1\}}{P\{ X\neq 1\}}$。
- $P\{ X\lt 2\cap X\neq 1\}=P\{ X=-1\}=0.4$。
- $P\{ X\neq 1\}=1-P\{ X=1\}=1-0.4=0.6$。
所以,$P\{ X\lt 2|X\neq 1\} =\frac{0.4}{0.6}=\frac{2}{3}$。
根据分布函数F(x)的定义,我们可以求出X取不同值的概率。对于离散型随机变量,分布函数F(x)在每个跳跃点处的跳跃值即为该点的概率。
- 当 $x=-1$ 时,$F(-1)=0.4$,所以 $P(X=-1)=0.4$。
- 当 $x=1$ 时,$F(1)=0.8$,所以 $P(X=1)=F(1)-F(-1)=0.8-0.4=0.4$。
- 当 $x=3$ 时,$F(3)=1$,所以 $P(X=3)=F(3)-F(1)=1-0.8=0.2$。
步骤 2:求 $P\{ X\lt 2|X\neq 1\} $
根据条件概率的定义,$P\{ X\lt 2|X\neq 1\} =\frac{P\{ X\lt 2\cap X\neq 1\}}{P\{ X\neq 1\}}$。
- $P\{ X\lt 2\cap X\neq 1\}=P\{ X=-1\}=0.4$。
- $P\{ X\neq 1\}=1-P\{ X=1\}=1-0.4=0.6$。
所以,$P\{ X\lt 2|X\neq 1\} =\frac{0.4}{0.6}=\frac{2}{3}$。