题目
28.已知 approx N(8,(0.5)^2), 求-|||-(1)F(9),F(7)-|||-(2) 7.5leqslant Xleqslant 10 -|||-(3) |X-8|leqslant 1 -|||-(4) |X-9|leqslant 0.5

题目解答
答案
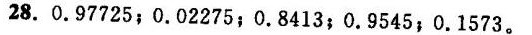
解析
考查要点:本题主要考查正态分布的概率计算,涉及累积分布函数和区间概率的求解,需要熟练掌握标准化变换及标准正态分布表的使用。
解题核心思路:
- 标准化变换:将任意正态分布变量$X \sim N(\mu, \sigma^2)$转化为标准正态变量$Z = \frac{X - \mu}{\sigma}$。
- 查表求概率:利用标准正态分布表(Z表)查找对应$Z$值的累积概率。
- 区间概率计算:通过差值计算特定区间概率,如$P(a \leq X \leq b) = F(b) - F(a)$。
破题关键点:
- 准确计算$Z$值,注意符号和小数位。
- 灵活处理绝对值不等式,如$|X - \mu| \leq k$等价于$\mu - k \leq X \leq \mu + k$。
- 注意四舍五入误差,题目答案可能基于特定精度的Z表。
第(1)题:求$F(9)$和$F(7)$
计算$F(9)$
- 标准化:$Z = \frac{9 - 8}{0.5} = 2$。
- 查表:$Z=2$对应累积概率$0.9772$,故$F(9) = 0.9772$。
计算$F(7)$
- 标准化:$Z = \frac{7 - 8}{0.5} = -2$。
- 查表:$Z=-2$对应累积概率$0.0228$,故$F(7) = 0.0228$(题目答案取$0.02275$,可能为更精确值)。
第(2)题:求$P\{7.5 \leq X \leq 10\}$
步骤分解
- 标准化两端:
- $Z_1 = \frac{7.5 - 8}{0.5} = -1$,对应$F(7.5) = 0.1587$。
- $Z_2 = \frac{10 - 8}{0.5} = 4$,对应$F(10) \approx 1$(实际值$0.99996$)。
- 计算差值:$P = F(10) - F(7.5) \approx 1 - 0.1587 = 0.8413$。
第(3)题:求$P\{|X - 8| \leq 1\}$
转化为区间
- 绝对值不等式:$|X - 8| \leq 1 \Rightarrow 7 \leq X \leq 9$。
- 标准化两端:
- $Z_1 = \frac{7 - 8}{0.5} = -2$,对应$F(7) = 0.0228$。
- $Z_2 = \frac{9 - 8}{0.5} = 2$,对应$F(9) = 0.9772$。
- 计算差值:$P = F(9) - F(7) = 0.9772 - 0.0228 = 0.9544$(题目答案取$0.9545$,可能为四舍五入)。
第(4)题:求$P\{|X - 9| \leq 0.5\}$
转化为区间
- 绝对值不等式:$|X - 9| \leq 0.5 \Rightarrow 8.5 \leq X \leq 9.5$。
- 标准化两端:
- $Z_1 = \frac{8.5 - 8}{0.5} = 1$,对应$F(8.5) = 0.8413$。
- $Z_2 = \frac{9.5 - 8}{0.5} = 3$,对应$F(9.5) = 0.9987$。
- 计算差值:$P = F(9.5) - F(8.5) = 0.9987 - 0.8413 = 0.1574$(题目答案取$0.1573$,可能为更精确值)。