求直线 ) x+y-z-1=0 x-y+z+1=0 .在平面x+y+z=0上的投影直线的方程。
求直线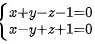 在平面x+y+z=0上的投影直线的方程。
在平面x+y+z=0上的投影直线的方程。
题目解答
答案
解:应用平面束的方法,设过直线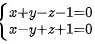 的平面束方程为
的平面束方程为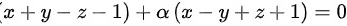
即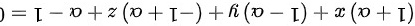
这平面与已知平面x+y+z=0垂直的条件是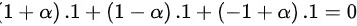
解得: ,代入平面束方程中得投影平面方程为y-z-1=0,所以投影直线为
,代入平面束方程中得投影平面方程为y-z-1=0,所以投影直线为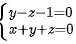 .
.
解析
考查要点:本题主要考查空间几何中直线在平面上的投影方程求解方法,涉及平面束方程的应用及平面垂直条件的运用。
解题核心思路:
- 平面束方程:过已知直线的所有平面可表示为两个平面方程的线性组合。
- 垂直条件:投影平面需与原平面垂直,通过法向量点积为零确定参数。
- 联立方程:投影直线是投影平面与原平面的交线,联立两平面方程即可得到结果。
破题关键点:
- 正确写出平面束方程,并利用垂直条件求解参数。
- 联立投影平面与原平面方程,得到投影直线的方程。
步骤1:确定平面束方程
已知直线由平面方程联立:
$\begin{cases}x + y - z - 1 = 0 \\x - y + z + 1 = 0\end{cases}$
平面束方程为:
$(x + y - z - 1) + \alpha (x - y + z + 1) = 0$
展开整理得:
$(1+\alpha)x + (1-\alpha)y + (-1+\alpha)z + (\alpha - 1) = 0$
步骤2:平面垂直条件
投影平面需与原平面 $x + y + z = 0$ 垂直,其法向量为 $(1,1,1)$。平面束的法向量为 $(1+\alpha, 1-\alpha, -1+\alpha)$,垂直条件为:
$(1+\alpha) \cdot 1 + (1-\alpha) \cdot 1 + (-1+\alpha) \cdot 1 = 0$
解得:
$1 + \alpha = 0 \quad \Rightarrow \quad \alpha = -1$
步骤3:确定投影平面方程
将 $\alpha = -1$ 代入平面束方程:
$0 \cdot x + 2y - 2z - 2 = 0 \quad \Rightarrow \quad y - z - 1 = 0$
步骤4:联立求投影直线
投影直线是投影平面 $y - z - 1 = 0$ 与原平面 $x + y + z = 0$ 的交线,联立得:
$\begin{cases}y - z - 1 = 0 \\x + y + z = 0\end{cases}$