题目
设V1与V2分别是齐次方程组 _(1)+(x)_(2)+... +(x)_(n)=0 与-|||-_(1)=(x)_(2)=... =(x)_(n) 的解空间,证明: ^n=(V)_(1)+(V)_(2)
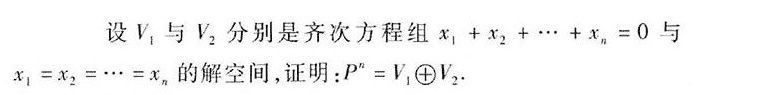
题目解答
答案

解析
考查要点:本题主要考查齐次方程组解空间的直和分解,涉及解空间的维数、向量空间的分解方法以及直和的判定条件。
解题核心思路:
- 分解任意向量:将任意向量分解为属于V1和V2的两个部分之和,证明V1 + V2 = Pⁿ。
- 维数分析:利用维数公式,结合V1和V2的维数之和等于Pⁿ的维数,且它们的交集为{0},从而得出直和结论。
破题关键点:
- V1的维数:由方程x₁ + x₂ + … + xₙ = 0确定,维数为n−1。
- V2的维数:由所有分量相等的条件确定,维数为1。
- 分解方法:将任意向量分解为“平均值向量”(属于V2)和“偏差向量”(属于V1)。
步骤1:分解任意向量
任取α = (a₁, a₂, ..., aₙ) ∈ Pⁿ,定义:
- V2部分:取平均值向量$\mathbf{v_2} = \left( \frac{1}{n}\sum_{i=1}^{n}a_i, \frac{1}{n}\sum_{i=1}^{n}a_i, \dots, \frac{1}{n}\sum_{i=1}^{n}a_i \right)$,显然$\mathbf{v_2} \in V_2$。
- V1部分:定义$\mathbf{v_1} = \alpha - \mathbf{v_2} = \left( a_1 - \frac{1}{n}\sum_{i=1}^{n}a_i, \dots, a_n - \frac{1}{n}\sum_{i=1}^{n}a_i \right)$。验证$\mathbf{v_1}$满足V1的条件:
$\sum_{i=1}^{n} \left( a_i - \frac{1}{n}\sum_{j=1}^{n}a_j \right) = \sum_{i=1}^{n}a_i - n \cdot \frac{1}{n}\sum_{j=1}^{n}a_j = 0.$
因此$\mathbf{v_1} \in V_1$,且$\alpha = \mathbf{v_1} + \mathbf{v_2}$,故$P^n = V_1 + V_2$。
步骤2:证明交集为{0}
若向量$\mathbf{v} \in V_1 \cap V_2$,则其分量全等且和为0。设$\mathbf{v} = (c, c, \dots, c)$,则:
$\sum_{i=1}^{n}c = nc = 0 \implies c = 0.$
故$V_1 \cap V_2 = \{0\}$。
步骤3:维数验证
- $\dim(V_1) = n-1$,$\dim(V_2) = 1$。
- 由维数公式:
$\dim(V_1 + V_2) + \dim(V_1 \cap V_2) = \dim(V_1) + \dim(V_2).$
代入得$\dim(V_1 + V_2) = n$,结合$V_1 + V_2 \subseteq P^n$,故$V_1 + V_2 = P^n$且为直和。