题目
设A . B为任意的两个事件,P(A) =0.5,P(B) =0.2,P(B-A) =0.1,求P(AB) ,(Aoverline (B)) ,P(AUB) ,(Aoverline (B)) ,(Aoverline (B))
设A . B为任意的两个事件,P(A) =0.5,P(B) =0.2,P(B-A) =0.1,求P(AB) ,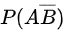 ,P(AUB) ,
,P(AUB) ,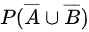 ,
,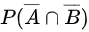
题目解答
答案
首先,根据概率的减法公式,我们有:
P(A - B) = P(A) - P(AB)
但题目中并没有给出P(A - B)的具体值,不过我们可以利用P(B - A)的值来间接求解P(AB)。
由于P(B - A) = P(B) - P(AB),我们可以得到:
(1)P(AB) = P(B) - P(B - A) = 0.2 - 0.1 = 0.1
(2)
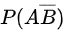 = P(A) - P(AB) = 0.5 - 0.1 = 0.4
(3)P(AUB) = P(A) + P(B) - P(AB)
= P(A) - P(AB) = 0.5 - 0.1 = 0.4
(3)P(AUB) = P(A) + P(B) - P(AB)
= 0.5 + 0.2 - 0.1 = 0.6
(4)
由于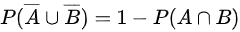 ,并且
,并且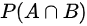 = P(AB) = 0.1,所以:
= P(AB) = 0.1,所以:
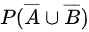 = 1 - 0.1 = 0.9
= 1 - 0.1 = 0.9
(4)
由于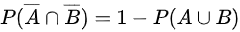 ,所以:
,所以:
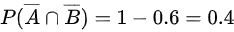
解析
步骤 1:求P(AB)
根据概率的减法公式,我们有:
P(B - A) = P(B) - P(AB)
所以,P(AB) = P(B) - P(B - A) = 0.2 - 0.1 = 0.1
步骤 2:求$P(A\overline {B})$
$P(A\overline {B})$= P(A) - P(AB) = 0.5 - 0.1 = 0.4
步骤 3:求P(AUB)
P(AUB) = P(A) + P(B) - P(AB)
= 0.5 + 0.2 - 0.1 = 0.6
步骤 4:求$P(\overline {A}\cup \overline {B})$
$P(\overline {A}\cup \overline {B})=1-P(A\cap B)$,并且$P(A\cap B)$= P(AB) = 0.1,所以:
$P(\overline {A}\cup \overline {B})$= 1 - 0.1 = 0.9
步骤 5:求$P(\overline {A}\cap \overline {B})$
$P(\overline {A}\cap \overline {B})=1-P(A\cup B)$,所以:
$P(\overline {A}\cap \overline {B})=1-0.6=0.4$
根据概率的减法公式,我们有:
P(B - A) = P(B) - P(AB)
所以,P(AB) = P(B) - P(B - A) = 0.2 - 0.1 = 0.1
步骤 2:求$P(A\overline {B})$
$P(A\overline {B})$= P(A) - P(AB) = 0.5 - 0.1 = 0.4
步骤 3:求P(AUB)
P(AUB) = P(A) + P(B) - P(AB)
= 0.5 + 0.2 - 0.1 = 0.6
步骤 4:求$P(\overline {A}\cup \overline {B})$
$P(\overline {A}\cup \overline {B})=1-P(A\cap B)$,并且$P(A\cap B)$= P(AB) = 0.1,所以:
$P(\overline {A}\cup \overline {B})$= 1 - 0.1 = 0.9
步骤 5:求$P(\overline {A}\cap \overline {B})$
$P(\overline {A}\cap \overline {B})=1-P(A\cup B)$,所以:
$P(\overline {A}\cap \overline {B})=1-0.6=0.4$