题目
设连续型随机变量X的概率密度函数为f(x)= { x+1,0leqslant xleqslant 2 0,else ..
设连续型随机变量X的概率密度函数为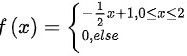 ,求
,求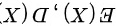 .
.
题目解答
答案
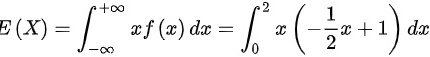
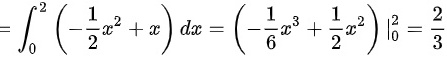 ,
,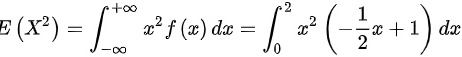
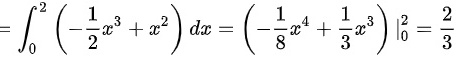 ,则
,则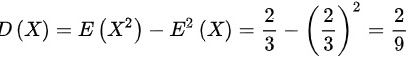 .
.
解析
步骤 1:计算E(X)
E(X)是随机变量X的期望值,计算公式为E(X) = $\int_{-\infty}^{\infty} x f(x) dx$。对于给定的概率密度函数f(x),我们只在0到2的区间内积分,因为在这个区间外f(x) = 0。
E(X) = $\int_{0}^{2} x(-\dfrac{1}{2}x + 1) dx$ = $\int_{0}^{2} (-\dfrac{1}{2}x^2 + x) dx$ = $[-\dfrac{1}{6}x^3 + \dfrac{1}{2}x^2]_{0}^{2}$ = $-\dfrac{1}{6}(2)^3 + \dfrac{1}{2}(2)^2$ = $-\dfrac{4}{6} + 2$ = $\dfrac{2}{3}$。
步骤 2:计算E(X^2)
E(X^2)是随机变量X的平方的期望值,计算公式为E(X^2) = $\int_{-\infty}^{\infty} x^2 f(x) dx$。同样地,我们只在0到2的区间内积分。
E(X^2) = $\int_{0}^{2} x^2(-\dfrac{1}{2}x + 1) dx$ = $\int_{0}^{2} (-\dfrac{1}{2}x^3 + x^2) dx$ = $[-\dfrac{1}{8}x^4 + \dfrac{1}{3}x^3]_{0}^{2}$ = $-\dfrac{1}{8}(2)^4 + \dfrac{1}{3}(2)^3$ = $-\dfrac{16}{8} + \dfrac{8}{3}$ = $-\dfrac{2}{1} + \dfrac{8}{3}$ = $\dfrac{2}{3}$。
步骤 3:计算D(X)
D(X)是随机变量X的方差,计算公式为D(X) = E(X^2) - [E(X)]^2。
D(X) = $\dfrac{2}{3} - (\dfrac{2}{3})^2$ = $\dfrac{2}{3} - \dfrac{4}{9}$ = $\dfrac{6}{9} - \dfrac{4}{9}$ = $\dfrac{2}{9}$。
E(X)是随机变量X的期望值,计算公式为E(X) = $\int_{-\infty}^{\infty} x f(x) dx$。对于给定的概率密度函数f(x),我们只在0到2的区间内积分,因为在这个区间外f(x) = 0。
E(X) = $\int_{0}^{2} x(-\dfrac{1}{2}x + 1) dx$ = $\int_{0}^{2} (-\dfrac{1}{2}x^2 + x) dx$ = $[-\dfrac{1}{6}x^3 + \dfrac{1}{2}x^2]_{0}^{2}$ = $-\dfrac{1}{6}(2)^3 + \dfrac{1}{2}(2)^2$ = $-\dfrac{4}{6} + 2$ = $\dfrac{2}{3}$。
步骤 2:计算E(X^2)
E(X^2)是随机变量X的平方的期望值,计算公式为E(X^2) = $\int_{-\infty}^{\infty} x^2 f(x) dx$。同样地,我们只在0到2的区间内积分。
E(X^2) = $\int_{0}^{2} x^2(-\dfrac{1}{2}x + 1) dx$ = $\int_{0}^{2} (-\dfrac{1}{2}x^3 + x^2) dx$ = $[-\dfrac{1}{8}x^4 + \dfrac{1}{3}x^3]_{0}^{2}$ = $-\dfrac{1}{8}(2)^4 + \dfrac{1}{3}(2)^3$ = $-\dfrac{16}{8} + \dfrac{8}{3}$ = $-\dfrac{2}{1} + \dfrac{8}{3}$ = $\dfrac{2}{3}$。
步骤 3:计算D(X)
D(X)是随机变量X的方差,计算公式为D(X) = E(X^2) - [E(X)]^2。
D(X) = $\dfrac{2}{3} - (\dfrac{2}{3})^2$ = $\dfrac{2}{3} - \dfrac{4}{9}$ = $\dfrac{6}{9} - \dfrac{4}{9}$ = $\dfrac{2}{9}$。