题目
47.将函数 dfrac (x+5)(2{x)^2-x-6} 展开成x的幂级数.
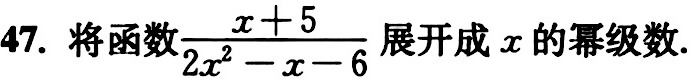
题目解答
答案
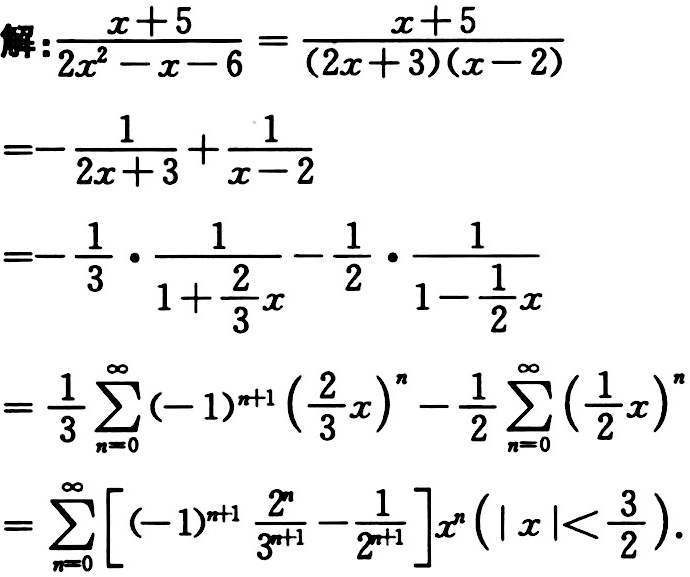
解析
步骤 1:分解分母
将分母 $2x^2 - x - 6$ 分解为 $(2x + 3)(x - 2)$,得到 $\dfrac {x+5}{2{x}^{2}-x-6}=\dfrac {x+5}{(2x+3)(x-2)}$。
步骤 2:部分分式分解
将 $\dfrac {x+5}{(2x+3)(x-2)}$ 分解为 $\dfrac {A}{2x+3} + \dfrac {B}{x-2}$,其中 $A$ 和 $B$ 是待定系数。通过解方程组确定 $A$ 和 $B$ 的值,得到 $\dfrac {x+5}{(2x+3)(x-2)}=-\dfrac {1}{2x+3}+\dfrac {1}{x-2}$。
步骤 3:幂级数展开
将 $-\dfrac {1}{2x+3}$ 和 $\dfrac {1}{x-2}$ 分别展开成幂级数。对于 $-\dfrac {1}{2x+3}$,可以写成 $-\dfrac {1}{3}\cdot \dfrac {1}{1+\dfrac {2}{3}x}$,然后利用几何级数公式展开。对于 $\dfrac {1}{x-2}$,可以写成 $-\dfrac {1}{2}\cdot \dfrac {1}{1-\dfrac {1}{2}x}$,然后利用几何级数公式展开。
步骤 4:合并幂级数
将两个幂级数合并,得到最终的幂级数表达式。
将分母 $2x^2 - x - 6$ 分解为 $(2x + 3)(x - 2)$,得到 $\dfrac {x+5}{2{x}^{2}-x-6}=\dfrac {x+5}{(2x+3)(x-2)}$。
步骤 2:部分分式分解
将 $\dfrac {x+5}{(2x+3)(x-2)}$ 分解为 $\dfrac {A}{2x+3} + \dfrac {B}{x-2}$,其中 $A$ 和 $B$ 是待定系数。通过解方程组确定 $A$ 和 $B$ 的值,得到 $\dfrac {x+5}{(2x+3)(x-2)}=-\dfrac {1}{2x+3}+\dfrac {1}{x-2}$。
步骤 3:幂级数展开
将 $-\dfrac {1}{2x+3}$ 和 $\dfrac {1}{x-2}$ 分别展开成幂级数。对于 $-\dfrac {1}{2x+3}$,可以写成 $-\dfrac {1}{3}\cdot \dfrac {1}{1+\dfrac {2}{3}x}$,然后利用几何级数公式展开。对于 $\dfrac {1}{x-2}$,可以写成 $-\dfrac {1}{2}\cdot \dfrac {1}{1-\dfrac {1}{2}x}$,然后利用几何级数公式展开。
步骤 4:合并幂级数
将两个幂级数合并,得到最终的幂级数表达式。