题目
设随机变量X的概率密度为fx(x),且fx(x),则随机变量Y的概率密度为_________.
设随机变量X的概率密度为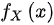 ,且
,且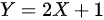 ,则随机变量Y的概率密度为_________.
,则随机变量Y的概率密度为_________.
题目解答
答案
随机变量X的概率密度为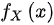 ,则
,则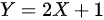 的分布函数为
的分布函数为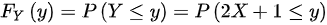
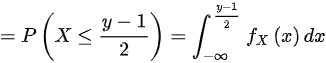 ,则随机变量Y的概率密度为
,则随机变量Y的概率密度为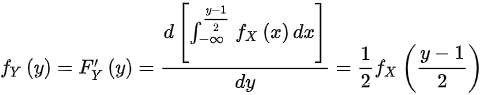 .
.
解析
步骤 1:确定Y的分布函数
随机变量X的概率密度为fx(x),则Y=2X+1的分布函数为$F'(y)=P(Y\leqslant y)=P(2x+1\leqslant y)$$=P(x\leqslant \dfrac {y-1}{2})={\int }_{-\infty }^{\dfrac {y-1}{2}}{f}_{x}(x)dx$。
步骤 2:求Y的概率密度
由分布函数$F'(y)$,求导得到Y的概率密度$f(y)$,即$f(y)={F}_{y}'(y)=\dfrac {d[ f'(x)}{dy}] d=\dfrac {d[ f'(x)dx] }{dy}$。
步骤 3:代入X的概率密度
将X的概率密度fx(x)代入到Y的概率密度表达式中,得到$f(y)=\dfrac {1}{2}fx(\dfrac {y-1}{2})$。
随机变量X的概率密度为fx(x),则Y=2X+1的分布函数为$F'(y)=P(Y\leqslant y)=P(2x+1\leqslant y)$$=P(x\leqslant \dfrac {y-1}{2})={\int }_{-\infty }^{\dfrac {y-1}{2}}{f}_{x}(x)dx$。
步骤 2:求Y的概率密度
由分布函数$F'(y)$,求导得到Y的概率密度$f(y)$,即$f(y)={F}_{y}'(y)=\dfrac {d[ f'(x)}{dy}] d=\dfrac {d[ f'(x)dx] }{dy}$。
步骤 3:代入X的概率密度
将X的概率密度fx(x)代入到Y的概率密度表达式中,得到$f(y)=\dfrac {1}{2}fx(\dfrac {y-1}{2})$。