题目
(2)求微分方程 '+y=(e)^-x 的通解.
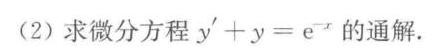
题目解答
答案
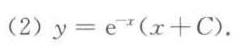
解析
步骤 1:识别方程类型
这是一个一阶线性非齐次微分方程,形式为 $y' + P(x)y = Q(x)$,其中 $P(x) = 1$,$Q(x) = e^{-x}$。
步骤 2:求解对应的齐次方程
对应的齐次方程为 $y' + y = 0$。这是一个可分离变量的方程,分离变量后得 $\frac{dy}{y} = -dx$。积分得 $\ln|y| = -x + C$,即 $y = Ce^{-x}$,其中 $C$ 是积分常数。
步骤 3:求非齐次方程的特解
使用常数变易法,设非齐次方程的特解为 $y = u(x)e^{-x}$,其中 $u(x)$ 是待定函数。将 $y = u(x)e^{-x}$ 代入原方程,得 $u'(x)e^{-x} = e^{-x}$,即 $u'(x) = 1$。积分得 $u(x) = x + C$,其中 $C$ 是积分常数。因此,特解为 $y = (x + C)e^{-x}$。
步骤 4:写出通解
通解为齐次方程的通解加上非齐次方程的特解,即 $y = Ce^{-x} + (x + C)e^{-x} = (x + C)e^{-x}$,其中 $C$ 是任意常数。
这是一个一阶线性非齐次微分方程,形式为 $y' + P(x)y = Q(x)$,其中 $P(x) = 1$,$Q(x) = e^{-x}$。
步骤 2:求解对应的齐次方程
对应的齐次方程为 $y' + y = 0$。这是一个可分离变量的方程,分离变量后得 $\frac{dy}{y} = -dx$。积分得 $\ln|y| = -x + C$,即 $y = Ce^{-x}$,其中 $C$ 是积分常数。
步骤 3:求非齐次方程的特解
使用常数变易法,设非齐次方程的特解为 $y = u(x)e^{-x}$,其中 $u(x)$ 是待定函数。将 $y = u(x)e^{-x}$ 代入原方程,得 $u'(x)e^{-x} = e^{-x}$,即 $u'(x) = 1$。积分得 $u(x) = x + C$,其中 $C$ 是积分常数。因此,特解为 $y = (x + C)e^{-x}$。
步骤 4:写出通解
通解为齐次方程的通解加上非齐次方程的特解,即 $y = Ce^{-x} + (x + C)e^{-x} = (x + C)e^{-x}$,其中 $C$ 是任意常数。