题目
设随机变量×在区间×上服从均匀分布,求×的概率密度函数。
设随机变量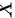 在区间
在区间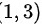 上服从均匀分布,求
上服从均匀分布,求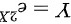 的概率密度函数。
的概率密度函数。
题目解答
答案
首先明确取值范围: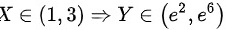 。考虑分布函数
。考虑分布函数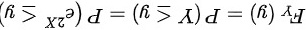 ,由于单调性可以等价写出
,由于单调性可以等价写出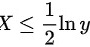 ,所以
,所以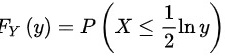 。在均匀分布下这个概率等于
。在均匀分布下这个概率等于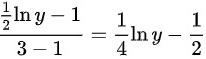 ,所以
,所以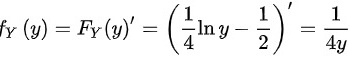 。这对应的区间是
。这对应的区间是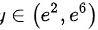 ,在其余部分上函数值为0,所以答案是
,在其余部分上函数值为0,所以答案是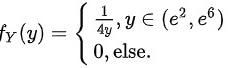 。
。
解析
步骤 1:确定随机变量X的取值范围
随机变量X在区间(1,3)上服从均匀分布,即$X\in (1,3)$。
步骤 2:确定随机变量Y的取值范围
由于$Y={e}^{2X}$,当$X\in (1,3)$时,$Y\in ({e}^{2},{e}^{6})$。
步骤 3:计算Y的分布函数
分布函数${F}_{Y}(y)=P(Y\leqslant y)=P({e}^{2x}\leqslant y)$,由于${e}^{2x}$是单调递增函数,可以等价写出$X\leqslant \dfrac {1}{2}\ln y$,所以${F}_{Y}(y)=P(X\leqslant \dfrac {1}{2}\ln y)$。
步骤 4:计算分布函数${F}_{Y}(y)$
在均匀分布下,$P(X\leqslant \dfrac {1}{2}\ln y)=\dfrac {\dfrac {1}{2}\ln y-1}{3-1}=\dfrac {1}{4}\ln y-\dfrac {1}{2}$。
步骤 5:计算概率密度函数$f(y)$
$f(y)={F}_{Y}(y)'=(\dfrac {1}{4}\ln y-\dfrac {1}{2})'=\dfrac {1}{4y}$。这对应的区间是$y\in ({e}^{2},{e}^{6})$,在其余部分上函数值为0。
随机变量X在区间(1,3)上服从均匀分布,即$X\in (1,3)$。
步骤 2:确定随机变量Y的取值范围
由于$Y={e}^{2X}$,当$X\in (1,3)$时,$Y\in ({e}^{2},{e}^{6})$。
步骤 3:计算Y的分布函数
分布函数${F}_{Y}(y)=P(Y\leqslant y)=P({e}^{2x}\leqslant y)$,由于${e}^{2x}$是单调递增函数,可以等价写出$X\leqslant \dfrac {1}{2}\ln y$,所以${F}_{Y}(y)=P(X\leqslant \dfrac {1}{2}\ln y)$。
步骤 4:计算分布函数${F}_{Y}(y)$
在均匀分布下,$P(X\leqslant \dfrac {1}{2}\ln y)=\dfrac {\dfrac {1}{2}\ln y-1}{3-1}=\dfrac {1}{4}\ln y-\dfrac {1}{2}$。
步骤 5:计算概率密度函数$f(y)$
$f(y)={F}_{Y}(y)'=(\dfrac {1}{4}\ln y-\dfrac {1}{2})'=\dfrac {1}{4y}$。这对应的区间是$y\in ({e}^{2},{e}^{6})$,在其余部分上函数值为0。