题目
若随机变量的概率密度为,求:①常数; ②落在 区间内的概率; ③的分布函数。
若随机变量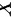 的概率密度为
的概率密度为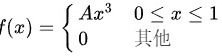 ,求:
,求:
①常数 ;
;
②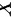 落在
落在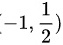 区间内的概率;
区间内的概率;
③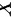 的分布函数
的分布函数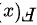 。
。
题目解答
答案
① 因为随机变量的概率密度函数在整个定义域上的积分值为1,所以有:
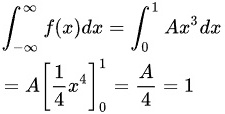
解得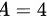 .
.
②  落在
落在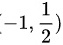 区间内的概率为:
区间内的概率为:
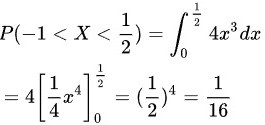
③ 当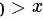 时,
时,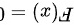 ;
;
当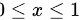 时,
时,
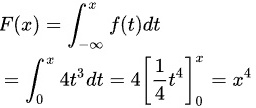
当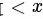 1" data-width="48" data-height="19" data-size="571" data-format="png" style="max-width:100%">时,
1" data-width="48" data-height="19" data-size="571" data-format="png" style="max-width:100%">时,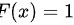 .
.
故分布函数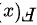 为:
为:
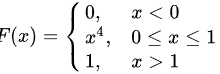 1 \end{cases}" data-width="225" data-height="74" data-size="4375" data-format="png" style="max-width:100%">.
1 \end{cases}" data-width="225" data-height="74" data-size="4375" data-format="png" style="max-width:100%">.
故答案为:
(1)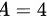 ;(2)
;(2)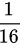 ;
;
(3)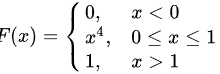 1 \end{cases}" data-width="225" data-height="74" data-size="4375" data-format="png" style="max-width:100%">.
1 \end{cases}" data-width="225" data-height="74" data-size="4375" data-format="png" style="max-width:100%">.
解析
步骤 1:求常数A
因为随机变量的概率密度函数在整个定义域上的积分值为1,所以有:
$$
\int_{-\infty}^{\infty} f(x) dx = 1
$$
由于$f(x)$在$0\leqslant x\leqslant 1$区间内为$Ax^3$,在其他区间内为0,所以积分可以简化为:
$$
\int_{0}^{1} Ax^3 dx = 1
$$
计算积分:
$$
A\int_{0}^{1} x^3 dx = A\left[\frac{1}{4}x^4\right]_{0}^{1} = A\left(\frac{1}{4} - 0\right) = \frac{A}{4}
$$
所以有:
$$
\frac{A}{4} = 1
$$
解得:
$$
A = 4
$$
步骤 2:求落在$(-1,\dfrac {1}{2})$ 区间内的概率
由于$f(x)$在$0\leqslant x\leqslant 1$区间内为$4x^3$,在其他区间内为0,所以落在$(-1,\dfrac {1}{2})$ 区间内的概率为:
$$
P(-1$$
计算积分:
$$
\int_{0}^{\frac{1}{2}} 4x^3 dx = 4\left[\frac{1}{4}x^4\right]_{0}^{\frac{1}{2}} = 4\left(\frac{1}{4}\left(\frac{1}{2}\right)^4 - 0\right) = \left(\frac{1}{2}\right)^4 = \frac{1}{16}
$$
步骤 3:求分布函数$F(x)$
分布函数$F(x)$定义为:
$$
F(x) = P(X \leq x) = \int_{-\infty}^{x} f(t) dt
$$
当$x < 0$时,$f(x) = 0$,所以$F(x) = 0$。
当$0 \leq x \leq 1$时,$f(x) = 4x^3$,所以:
$$
F(x) = \int_{-\infty}^{x} f(t) dt = \int_{0}^{x} 4t^3 dt = 4\left[\frac{1}{4}t^4\right]_{0}^{x} = x^4
$$
当$x > 1$时,$f(x) = 0$,所以$F(x) = 1$。
综上所述,分布函数$F(x)$为:
$$
F(x) = \begin{cases}
0, & x < 0 \\
x^4, & 0 \leq x \leq 1 \\
1, & x > 1
\end{cases}
$$
因为随机变量的概率密度函数在整个定义域上的积分值为1,所以有:
$$
\int_{-\infty}^{\infty} f(x) dx = 1
$$
由于$f(x)$在$0\leqslant x\leqslant 1$区间内为$Ax^3$,在其他区间内为0,所以积分可以简化为:
$$
\int_{0}^{1} Ax^3 dx = 1
$$
计算积分:
$$
A\int_{0}^{1} x^3 dx = A\left[\frac{1}{4}x^4\right]_{0}^{1} = A\left(\frac{1}{4} - 0\right) = \frac{A}{4}
$$
所以有:
$$
\frac{A}{4} = 1
$$
解得:
$$
A = 4
$$
步骤 2:求落在$(-1,\dfrac {1}{2})$ 区间内的概率
由于$f(x)$在$0\leqslant x\leqslant 1$区间内为$4x^3$,在其他区间内为0,所以落在$(-1,\dfrac {1}{2})$ 区间内的概率为:
$$
P(-1
计算积分:
$$
\int_{0}^{\frac{1}{2}} 4x^3 dx = 4\left[\frac{1}{4}x^4\right]_{0}^{\frac{1}{2}} = 4\left(\frac{1}{4}\left(\frac{1}{2}\right)^4 - 0\right) = \left(\frac{1}{2}\right)^4 = \frac{1}{16}
$$
步骤 3:求分布函数$F(x)$
分布函数$F(x)$定义为:
$$
F(x) = P(X \leq x) = \int_{-\infty}^{x} f(t) dt
$$
当$x < 0$时,$f(x) = 0$,所以$F(x) = 0$。
当$0 \leq x \leq 1$时,$f(x) = 4x^3$,所以:
$$
F(x) = \int_{-\infty}^{x} f(t) dt = \int_{0}^{x} 4t^3 dt = 4\left[\frac{1}{4}t^4\right]_{0}^{x} = x^4
$$
当$x > 1$时,$f(x) = 0$,所以$F(x) = 1$。
综上所述,分布函数$F(x)$为:
$$
F(x) = \begin{cases}
0, & x < 0 \\
x^4, & 0 \leq x \leq 1 \\
1, & x > 1
\end{cases}
$$