题目
设随机变量X服从参数为5的泊松分布,backsim Delta B(10,dfrac (1)(4)),且X,Y相互独立,则backsim Delta B(10,dfrac (1)(4))A.12.5B.2035C.2000D.35
设随机变量X服从参数为5的泊松分布,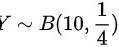 ,且X,Y相互独立,则
,且X,Y相互独立,则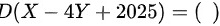
A.12.5
B.2035
C.2000
D.35
题目解答
答案
随机变量X服从参数为5的泊松分布,则泊松分布的参数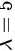 ,则X的数学期望为
,则X的数学期望为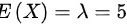 ,方差
,方差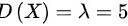 ,
,
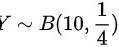 表示随机变量Y服从
表示随机变量Y服从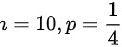 的二项分布,则Y的数学期望为
的二项分布,则Y的数学期望为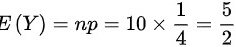 ,方差为
,方差为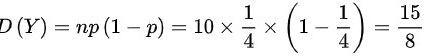 ,X,Y相互独立,则
,X,Y相互独立,则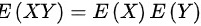 ,
,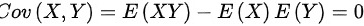 ,则
,则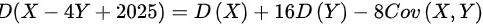
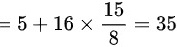 ,因此选择D。
,因此选择D。
解析
步骤 1:确定泊松分布的参数
随机变量X服从参数为5的泊松分布,因此泊松分布的参数$\lambda =5$。泊松分布的数学期望和方差都等于参数$\lambda$,即$E(X)=D(X)=5$。
步骤 2:确定二项分布的参数
$D\sim B(10,\dfrac {1}{4})$表示随机变量Y服从$z=10$ $p=\dfrac {1}{4}$的二项分布。二项分布的数学期望$E(Y)=np=10\times \dfrac {1}{4}=\dfrac {5}{2}$,方差$D(Y)=np(1-p)=10\times \dfrac {1}{4}\times (1-\dfrac {1}{4})=\dfrac {15}{8}$。
步骤 3:计算D(X-4Y+2025)
由于X和Y相互独立,因此$Cov(X,Y)=0$。根据方差的性质,$D(X-4Y+2025)=D(X)+16D(Y)-8Cov(X,Y)$。将已知的方差值代入,得到$D(X-4Y+2025)=5+16\times \dfrac {15}{8}=5+30=35$。
随机变量X服从参数为5的泊松分布,因此泊松分布的参数$\lambda =5$。泊松分布的数学期望和方差都等于参数$\lambda$,即$E(X)=D(X)=5$。
步骤 2:确定二项分布的参数
$D\sim B(10,\dfrac {1}{4})$表示随机变量Y服从$z=10$ $p=\dfrac {1}{4}$的二项分布。二项分布的数学期望$E(Y)=np=10\times \dfrac {1}{4}=\dfrac {5}{2}$,方差$D(Y)=np(1-p)=10\times \dfrac {1}{4}\times (1-\dfrac {1}{4})=\dfrac {15}{8}$。
步骤 3:计算D(X-4Y+2025)
由于X和Y相互独立,因此$Cov(X,Y)=0$。根据方差的性质,$D(X-4Y+2025)=D(X)+16D(Y)-8Cov(X,Y)$。将已知的方差值代入,得到$D(X-4Y+2025)=5+16\times \dfrac {15}{8}=5+30=35$。