题目
求过 点(1,1,1)且与直线 (1,1,1)垂直的平面方程
求过 点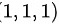
且与直线 
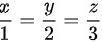垂直的平面方程
题目解答
答案
由题意，已知
直线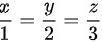
设其方向向量为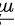
∴
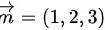
∵所求平面与直线 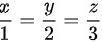垂直
∴平面的法向量即为该直线的方向向量
∵直线过点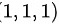
∴所求的平面方程为
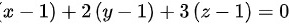
即，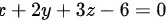
解析
步骤 1：确定直线的方向向量
直线 $\dfrac {x}{1}=\dfrac {y}{2}=\dfrac {z}{3}$ 的方向向量为 $\overrightarrow {m}=(1,2,3)$，因为直线的方向向量可以由直线方程的系数直接得到。
步骤 2：确定平面的法向量
由于所求平面与直线垂直，所以平面的法向量即为直线的方向向量，即 $\overrightarrow {n}=(1,2,3)$。
步骤 3：利用点法式方程求平面方程
已知平面过点(1,1,1)，且法向量为 $\overrightarrow {n}=(1,2,3)$，根据点法式方程 $(x-x_0)+2(y-y_0)+3(z-z_0)=0$，代入点(1,1,1)得到平面方程。
直线 $\dfrac {x}{1}=\dfrac {y}{2}=\dfrac {z}{3}$ 的方向向量为 $\overrightarrow {m}=(1,2,3)$，因为直线的方向向量可以由直线方程的系数直接得到。
步骤 2：确定平面的法向量
由于所求平面与直线垂直，所以平面的法向量即为直线的方向向量，即 $\overrightarrow {n}=(1,2,3)$。
步骤 3：利用点法式方程求平面方程
已知平面过点(1,1,1)，且法向量为 $\overrightarrow {n}=(1,2,3)$，根据点法式方程 $(x-x_0)+2(y-y_0)+3(z-z_0)=0$，代入点(1,1,1)得到平面方程。