题目
将两信息分别编码为A和B传送出去,接收站收到时,A被误收作B的概率为0.02,而B被误收作A的概率为0.01,信息A与信息B传送的频繁程度为2:1,若接收站收到的信息是A,问原发信息是A的概率是多少?
将两信息分别编码为A和B传送出去,接收站收到时,A被误收作B的概率为0.02,而B被误收作A的概率为0.01,信息A与信息B传送的频繁程度为2:1,若接收站收到的信息是A,问原发信息是A的概率是多少?
题目解答
答案
原发信息是A,收到的信息也是A的概率为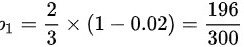 ,
,
原发信息是B,收到的信息是A的概率为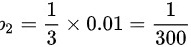 ,
,
则收到的信息是A的概率为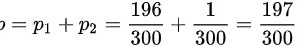 ,
,
接收站收到的信息是A,则原发信息是A的条件概率是 .
.
解析
步骤 1:定义事件
设事件A表示“原发信息是A”,事件B表示“原发信息是B”,事件C表示“收到的信息是A”。
步骤 2:计算原发信息是A且收到的信息也是A的概率
原发信息是A,收到的信息也是A的概率为$P(C|A) = 1 - 0.02 = 0.98$。
步骤 3:计算原发信息是B且收到的信息是A的概率
原发信息是B,收到的信息是A的概率为$P(C|B) = 0.01$。
步骤 4:计算原发信息是A的概率
原发信息是A的概率为$P(A) = \dfrac{2}{3}$。
步骤 5:计算原发信息是B的概率
原发信息是B的概率为$P(B) = \dfrac{1}{3}$。
步骤 6:计算收到的信息是A的概率
收到的信息是A的概率为$P(C) = P(C|A)P(A) + P(C|B)P(B) = 0.98 \times \dfrac{2}{3} + 0.01 \times \dfrac{1}{3} = \dfrac{196}{300} + \dfrac{1}{300} = \dfrac{197}{300}$。
步骤 7:计算原发信息是A且收到的信息是A的条件概率
原发信息是A且收到的信息是A的条件概率为$P(A|C) = \dfrac{P(C|A)P(A)}{P(C)} = \dfrac{0.98 \times \dfrac{2}{3}}{\dfrac{197}{300}} = \dfrac{196}{197}$。
设事件A表示“原发信息是A”,事件B表示“原发信息是B”,事件C表示“收到的信息是A”。
步骤 2:计算原发信息是A且收到的信息也是A的概率
原发信息是A,收到的信息也是A的概率为$P(C|A) = 1 - 0.02 = 0.98$。
步骤 3:计算原发信息是B且收到的信息是A的概率
原发信息是B,收到的信息是A的概率为$P(C|B) = 0.01$。
步骤 4:计算原发信息是A的概率
原发信息是A的概率为$P(A) = \dfrac{2}{3}$。
步骤 5:计算原发信息是B的概率
原发信息是B的概率为$P(B) = \dfrac{1}{3}$。
步骤 6:计算收到的信息是A的概率
收到的信息是A的概率为$P(C) = P(C|A)P(A) + P(C|B)P(B) = 0.98 \times \dfrac{2}{3} + 0.01 \times \dfrac{1}{3} = \dfrac{196}{300} + \dfrac{1}{300} = \dfrac{197}{300}$。
步骤 7:计算原发信息是A且收到的信息是A的条件概率
原发信息是A且收到的信息是A的条件概率为$P(A|C) = \dfrac{P(C|A)P(A)}{P(C)} = \dfrac{0.98 \times \dfrac{2}{3}}{\dfrac{197}{300}} = \dfrac{196}{197}$。