题目
已知非齐次线性方程组 |} (x)_(1)+(x)_(2)+(x)_(3)+(x)_(4)=-1 4(x)_(1)+3(x)_(2)+5(x)_(3)-(x)_(4)=-1 a(x)_(1)+(x)_(2)+3(x)_(3) .,有3个线性无关的解,证明:(1)方程组系数矩阵A的秩 |} (x)_(1)+(x)_(2)+(x)_(3)+(x)_(4)=-1 4(x)_(1)+3(x)_(2)+5(x)_(3)-(x)_(4)=-1 a(x)_(1)+(x)_(2)+3(x)_(3) .;(2)当 |} (x)_(1)+(x)_(2)+(x)_(3)+(x)_(4)=-1 4(x)_(1)+3(x)_(2)+5(x)_(3)-(x)_(4)=-1 a(x)_(1)+(x)_(2)+3(x)_(3) .时, |} (x)_(1)+(x)_(2)+(x)_(3)+(x)_(4)=-1 4(x)_(1)+3(x)_(2)+5(x)_(3)-(x)_(4)=-1 a(x)_(1)+(x)_(2)+3(x)_(3) ..
已知非齐次线性方程组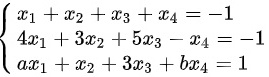 ,有3个线性无关的解,证明:
,有3个线性无关的解,证明:
(1)方程组系数矩阵A的秩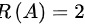 ;
;
(2)当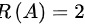 时,
时,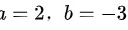 .
.
题目解答
答案
(1)因为该非齐次线性方程组有3个线性无关的解,因此对应的齐次线性方程组的解的个数应不少于2,有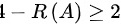 ,则有
,则有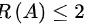 ,又因为A的行向量两两线性无关,故有
,又因为A的行向量两两线性无关,故有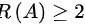 ,因此
,因此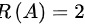 .
.
(2)对该方程组的增广矩阵进行初等行变换如下: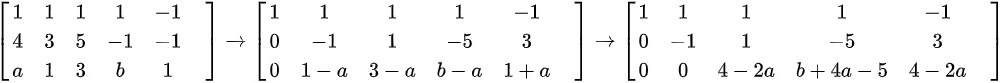 ,又因为
,又因为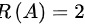 ,故有
,故有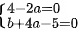 ,解得a=2,b=-3。
,解得a=2,b=-3。
解析
步骤 1:确定非齐次线性方程组的解的性质
非齐次线性方程组有3个线性无关的解,意味着对应的齐次线性方程组至少有2个线性无关的解。因此,齐次线性方程组的解空间的维数至少为2,即$1-R(A)\geqslant 2$,从而$R(A)\leqslant 2$。
步骤 2:确定系数矩阵A的秩
由于方程组的系数矩阵A的行向量两两线性无关,因此$R(A)\geqslant 2$。结合步骤1的结论,可以确定$R(A)=2$。
步骤 3:确定参数a和b的值
对非齐次线性方程组的增广矩阵进行初等行变换,得到:
$$
\left[\begin{array}{cccc|c}
1 & 1 & 1 & 1 & -1 \\
4 & 3 & 5 & -1 & -1 \\
a & 1 & 3 & 0 & b
\end{array}\right]
$$
进行初等行变换,得到:
$$
\left[\begin{array}{cccc|c}
1 & 1 & 1 & 1 & -1 \\
0 & -1 & 1 & -5 & 3 \\
0 & 1-a & 2-a & -a & b+a
\end{array}\right]
$$
由于$R(A)=2$,因此第三行必须是前两行的线性组合,即$b+4a-5=0$。解得$a=2$,$b=-3$。
非齐次线性方程组有3个线性无关的解,意味着对应的齐次线性方程组至少有2个线性无关的解。因此,齐次线性方程组的解空间的维数至少为2,即$1-R(A)\geqslant 2$,从而$R(A)\leqslant 2$。
步骤 2:确定系数矩阵A的秩
由于方程组的系数矩阵A的行向量两两线性无关,因此$R(A)\geqslant 2$。结合步骤1的结论,可以确定$R(A)=2$。
步骤 3:确定参数a和b的值
对非齐次线性方程组的增广矩阵进行初等行变换,得到:
$$
\left[\begin{array}{cccc|c}
1 & 1 & 1 & 1 & -1 \\
4 & 3 & 5 & -1 & -1 \\
a & 1 & 3 & 0 & b
\end{array}\right]
$$
进行初等行变换,得到:
$$
\left[\begin{array}{cccc|c}
1 & 1 & 1 & 1 & -1 \\
0 & -1 & 1 & -5 & 3 \\
0 & 1-a & 2-a & -a & b+a
\end{array}\right]
$$
由于$R(A)=2$,因此第三行必须是前两行的线性组合,即$b+4a-5=0$。解得$a=2$,$b=-3$。