题目
任意将10本书放在书架上,其中有两套书,一套3本,另一套4本,求下列事件的概率：(1)3本一套放在一起；(2)两套各自放在一起；(3)两套中至少有一套放在一起.
任意将10本书放在书架上,其中有两套书,一套3本,另一套4本,求下列事件的概率：
(1)3本一套放在一起；
(2)两套各自放在一起；
(3)两套中至少有一套放在一起.
题目解答
答案
(1)$$A_3^3\times A_8^8\div A_{10}^{10}=\frac{1}{15}$$
(2)$$A_3^3\times A_4^4\times A_5^5\div A_{10}^{10}=\frac{1}{210}$$
(3)先算出4本套在一起的概率$$A_4^4\times A_7^7\div A_{10}^{10}=\frac{1}{30}$$
同时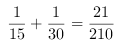
,
但这里面对于两套各方在一起重复一次,减(2)的结果,
应该是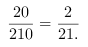
解析
步骤 1：计算3本一套放在一起的概率
将3本一套的书视为一个整体，与另外7本书一起排列，共有8个位置。3本一套的书内部可以有$A_3^3$种排列方式，而8个位置的排列方式有$A_8^8$种。因此，3本一套放在一起的排列方式有$A_3^3 \times A_8^8$种。总共有$A_{10}^{10}$种排列方式。所以，3本一套放在一起的概率为$A_3^3 \times A_8^8 \div A_{10}^{10}$。
步骤 2：计算两套各自放在一起的概率
将3本一套的书视为一个整体，4本一套的书视为另一个整体，与另外3本书一起排列，共有5个位置。3本一套的书内部可以有$A_3^3$种排列方式，4本一套的书内部可以有$A_4^4$种排列方式，而5个位置的排列方式有$A_5^5$种。因此，两套各自放在一起的排列方式有$A_3^3 \times A_4^4 \times A_5^5$种。总共有$A_{10}^{10}$种排列方式。所以，两套各自放在一起的概率为$A_3^3 \times A_4^4 \times A_5^5 \div A_{10}^{10}$。
步骤 3：计算两套中至少有一套放在一起的概率
首先计算4本一套放在一起的概率。将4本一套的书视为一个整体，与另外6本书一起排列，共有7个位置。4本一套的书内部可以有$A_4^4$种排列方式，而7个位置的排列方式有$A_7^7$种。因此，4本一套放在一起的排列方式有$A_4^4 \times A_7^7$种。总共有$A_{10}^{10}$种排列方式。所以，4本一套放在一起的概率为$A_4^4 \times A_7^7 \div A_{10}^{10}$。然后，将3本一套放在一起的概率和4本一套放在一起的概率相加，再减去两套各自放在一起的概率，得到两套中至少有一套放在一起的概率。
将3本一套的书视为一个整体，与另外7本书一起排列，共有8个位置。3本一套的书内部可以有$A_3^3$种排列方式，而8个位置的排列方式有$A_8^8$种。因此，3本一套放在一起的排列方式有$A_3^3 \times A_8^8$种。总共有$A_{10}^{10}$种排列方式。所以，3本一套放在一起的概率为$A_3^3 \times A_8^8 \div A_{10}^{10}$。
步骤 2：计算两套各自放在一起的概率
将3本一套的书视为一个整体，4本一套的书视为另一个整体，与另外3本书一起排列，共有5个位置。3本一套的书内部可以有$A_3^3$种排列方式，4本一套的书内部可以有$A_4^4$种排列方式，而5个位置的排列方式有$A_5^5$种。因此，两套各自放在一起的排列方式有$A_3^3 \times A_4^4 \times A_5^5$种。总共有$A_{10}^{10}$种排列方式。所以，两套各自放在一起的概率为$A_3^3 \times A_4^4 \times A_5^5 \div A_{10}^{10}$。
步骤 3：计算两套中至少有一套放在一起的概率
首先计算4本一套放在一起的概率。将4本一套的书视为一个整体，与另外6本书一起排列，共有7个位置。4本一套的书内部可以有$A_4^4$种排列方式，而7个位置的排列方式有$A_7^7$种。因此，4本一套放在一起的排列方式有$A_4^4 \times A_7^7$种。总共有$A_{10}^{10}$种排列方式。所以，4本一套放在一起的概率为$A_4^4 \times A_7^7 \div A_{10}^{10}$。然后，将3本一套放在一起的概率和4本一套放在一起的概率相加，再减去两套各自放在一起的概率，得到两套中至少有一套放在一起的概率。