题目
[例6]求过点 (3,1,-2) 且通过直线 dfrac (x-4)(5)=dfrac (y+3)(2)=dfrac (z)(1) 的平面方程.
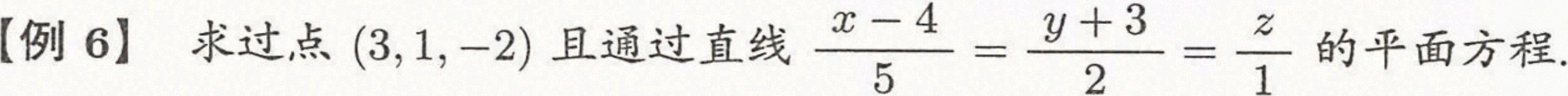
题目解答
答案

解析
考查要点:本题主要考查如何利用已知点和直线确定平面方程,涉及平面法向量的求解和点法式方程的应用。
解题思路:
- 确定平面法向量:通过已知点与直线上某点构成的向量,以及直线的方向向量,计算它们的叉积得到平面法向量。
- 代入点法式方程:利用法向量和已知点,写出平面方程。
- 平面束方程法(备选方法):利用直线的平面束方程,代入已知点确定参数,得到平面方程。
关键点:正确构造向量并计算叉积,或合理选择平面束方程并求解参数。
解法1:向量叉积法
步骤1:确定向量
- 已知点 $P(3,1,-2)$,直线上一点 $Q(4,-3,0)$,向量 $\overrightarrow{PQ} = (1,-4,2)$。
- 直线方向向量 $\mathbf{v} = (5,2,1)$。
步骤2:计算法向量
平面法向量 $\mathbf{n}$ 为 $\overrightarrow{PQ}$ 与 $\mathbf{v}$ 的叉积:
$\mathbf{n} = \begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\1 & -4 & 2 \\5 & 2 & 1\end{vmatrix} = (-8, 9, 22)$
步骤3:写出平面方程
用点法式方程:
$-8(x-3) + 9(y-1) + 22(z+2) = 0$
展开整理得:
$8x - 9y - 22z - 59 = 0$
解法2:平面束方程法
步骤1:构造平面束方程
直线可表示为:
$\frac{x-4}{5} = \frac{y+3}{2} = z$
对应平面束方程为:
$(x-5z-4) + \lambda(y-2z+3) = 0$
步骤2:代入已知点求参数
将点 $(3,1,-2)$ 代入方程:
$3 -5(-2) -4 + \lambda(1-2(-2)+3) = 0 \implies 9 + 8\lambda = 0 \implies \lambda = -\frac{9}{8}$
步骤3:确定平面方程
代入 $\lambda$ 得:
$8x - 9y - 22z - 59 = 0$