题目
设sin (x+2y-3z)=x+2y-3z，证明sin (x+2y-3z)=x+2y-3z.
设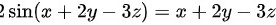
，证明
.
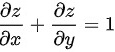题目解答
答案
由方程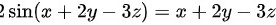，两边同时对
求导得：
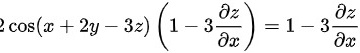
整理得：
两边同时对
求导得
整理得
即，得证。
解析
步骤 1：对$x$求偏导
给定方程$2\sin (x+2y-3z)=x+2y-3z$，我们首先对$x$求偏导。根据链式法则，我们有：
$$2\cos(x+2y-3z)\cdot(1-3\frac{\partial z}{\partial x})=1-3\frac{\partial z}{\partial x}$$
步骤 2：解出$\frac{\partial z}{\partial x}$
将上式整理，得到：
$$2\cos(x+2y-3z)-6\cos(x+2y-3z)\frac{\partial z}{\partial x}=1-3\frac{\partial z}{\partial x}$$
$$\Rightarrow 3\frac{\partial z}{\partial x}-6\cos(x+2y-3z)\frac{\partial z}{\partial x}=1-2\cos(x+2y-3z)$$
$$\Rightarrow \frac{\partial z}{\partial x}=\frac{1-2\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
步骤 3：对$y$求偏导
接下来，对$y$求偏导，同样使用链式法则：
$$2\cos(x+2y-3z)\cdot(2-3\frac{\partial z}{\partial y})=2-3\frac{\partial z}{\partial y}$$
步骤 4：解出$\frac{\partial z}{\partial y}$
将上式整理，得到：
$$4\cos(x+2y-3z)-6\cos(x+2y-3z)\frac{\partial z}{\partial y}=2-3\frac{\partial z}{\partial y}$$
$$\Rightarrow 3\frac{\partial z}{\partial y}-6\cos(x+2y-3z)\frac{\partial z}{\partial y}=2-4\cos(x+2y-3z)$$
$$\Rightarrow \frac{\partial z}{\partial y}=\frac{2-4\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
步骤 5：验证$\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}=1$
将$\frac{\partial z}{\partial x}$和$\frac{\partial z}{\partial y}$相加，得到：
$$\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}=\frac{1-2\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}+\frac{2-4\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
$$=\frac{3-6\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}=1$$
给定方程$2\sin (x+2y-3z)=x+2y-3z$，我们首先对$x$求偏导。根据链式法则，我们有：
$$2\cos(x+2y-3z)\cdot(1-3\frac{\partial z}{\partial x})=1-3\frac{\partial z}{\partial x}$$
步骤 2：解出$\frac{\partial z}{\partial x}$
将上式整理，得到：
$$2\cos(x+2y-3z)-6\cos(x+2y-3z)\frac{\partial z}{\partial x}=1-3\frac{\partial z}{\partial x}$$
$$\Rightarrow 3\frac{\partial z}{\partial x}-6\cos(x+2y-3z)\frac{\partial z}{\partial x}=1-2\cos(x+2y-3z)$$
$$\Rightarrow \frac{\partial z}{\partial x}=\frac{1-2\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
步骤 3：对$y$求偏导
接下来，对$y$求偏导，同样使用链式法则：
$$2\cos(x+2y-3z)\cdot(2-3\frac{\partial z}{\partial y})=2-3\frac{\partial z}{\partial y}$$
步骤 4：解出$\frac{\partial z}{\partial y}$
将上式整理，得到：
$$4\cos(x+2y-3z)-6\cos(x+2y-3z)\frac{\partial z}{\partial y}=2-3\frac{\partial z}{\partial y}$$
$$\Rightarrow 3\frac{\partial z}{\partial y}-6\cos(x+2y-3z)\frac{\partial z}{\partial y}=2-4\cos(x+2y-3z)$$
$$\Rightarrow \frac{\partial z}{\partial y}=\frac{2-4\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
步骤 5：验证$\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}=1$
将$\frac{\partial z}{\partial x}$和$\frac{\partial z}{\partial y}$相加，得到：
$$\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}=\frac{1-2\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}+\frac{2-4\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}$$
$$=\frac{3-6\cos(x+2y-3z)}{3-6\cos(x+2y-3z)}=1$$