题目
(int )_(0)^12xcos ((x)^2+1)dx= ( )A.cos 2- cos 1B.cos 2+ cos 1C.sin 2- sin 1D.sin 2+ sin 1
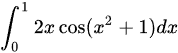 = ( )
= ( )
A.cos 2- cos 1
B.cos 2+ cos 1
C.sin 2- sin 1
D.sin 2+ sin 1
题目解答
答案
解:
∵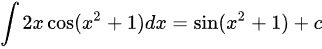 (c为常熟)
(c为常熟)
∴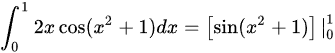
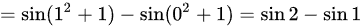
故答案为:C
解析
考查要点:本题主要考查定积分的换元法应用,特别是通过观察被积函数的结构,选择合适的中间变量进行替换,简化积分过程。
解题核心思路:
题目中的被积函数为$2x\cos(x^2+1)$,其中$2x$是$x^2+1$的导数,这提示我们可以使用第一类换元法(凑微分法)。通过令$u = x^2 + 1$,将原积分转化为关于$u$的简单积分,从而快速求解。
破题关键点:
- 识别被积函数的结构:发现$2x$与$x^2+1$的导数关系。
- 正确选择换元变量:令$u = x^2 + 1$,则$du = 2x dx$,直接将原积分转化为$\int \cos u \, du$。
- 代入上下限:换元后需将积分上下限从$x$的范围转换为$u$的范围,避免额外计算原函数后再代入$x$的值。
步骤1:选择换元变量
令$u = x^2 + 1$,则$du = 2x dx$,即$2x dx = du$。此时原积分可改写为:
$\int_{0}^{1} 2x \cos(x^2 + 1) dx = \int_{u(0)}^{u(1)} \cos u \, du$
步骤2:调整积分上下限
当$x = 0$时,$u = 0^2 + 1 = 1$;
当$x = 1$时,$u = 1^2 + 1 = 2$。
因此,积分变为:
$\int_{1}^{2} \cos u \, du$
步骤3:计算积分
积分$\int \cos u \, du = \sin u + C$,代入上下限得:
$\left. \sin u \right|_{1}^{2} = \sin 2 - \sin 1$
结论:最终结果为$\sin 2 - \sin 1$,对应选项C。