题目
.求由曲面 =sqrt (5-{x)^2-(y)^2} 及 ^2+(y)^2=4z 所围立体的体积.
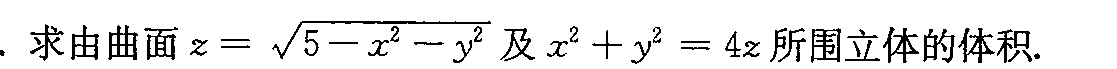
题目解答
答案

解析
步骤 1:确定曲面交线
首先,我们需要确定两个曲面的交线。给定的曲面是 $z=\sqrt {5-{x}^{2}-{y}^{2}}$ 和 ${x}^{2}+{y}^{2}=4z$。将这两个方程联立,可以得到交线的方程。
步骤 2:求解交线方程
将 $z=\sqrt {5-{x}^{2}-{y}^{2}}$ 代入 ${x}^{2}+{y}^{2}=4z$,得到 ${x}^{2}+{y}^{2}=4\sqrt {5-{x}^{2}-{y}^{2}}$。解这个方程,可以得到交线的方程为 $z=1$ 和 ${x}^{2}+{y}^{2}=4$。
步骤 3:确定积分区域
根据交线方程,可以确定积分区域。在 $xOy$ 平面上,积分区域为 ${x}^{2}+{y}^{2}\leqslant 4$,即 $0\leqslant \theta \leqslant 2\pi$ 和 $0\leqslant r\leqslant 2$。
步骤 4:转换为柱面坐标
将柱面坐标变换 $x=r\cos \theta$ 和 $y=r\sin \theta$ 代入积分区域,得到 $\dfrac {{x}^{2}+{y}^{2}}{4}\leqslant x\leqslant \sqrt {5-{x}^{2}-{y}^{2}}=\dfrac {{1}^{2}}{4}\leqslant x\leqslant \sqrt {5-{t}^{2}}$。
步骤 5:计算体积
利用柱面坐标计算体积,得到 $v= dv= 2π "dθ r2 rvs-2 r2 (√5-r^2-r^2/4)dr =π| 2 (√5-r^2-r/4 )d(r^2)]=2/3 π(5√5-4)$。
首先,我们需要确定两个曲面的交线。给定的曲面是 $z=\sqrt {5-{x}^{2}-{y}^{2}}$ 和 ${x}^{2}+{y}^{2}=4z$。将这两个方程联立,可以得到交线的方程。
步骤 2:求解交线方程
将 $z=\sqrt {5-{x}^{2}-{y}^{2}}$ 代入 ${x}^{2}+{y}^{2}=4z$,得到 ${x}^{2}+{y}^{2}=4\sqrt {5-{x}^{2}-{y}^{2}}$。解这个方程,可以得到交线的方程为 $z=1$ 和 ${x}^{2}+{y}^{2}=4$。
步骤 3:确定积分区域
根据交线方程,可以确定积分区域。在 $xOy$ 平面上,积分区域为 ${x}^{2}+{y}^{2}\leqslant 4$,即 $0\leqslant \theta \leqslant 2\pi$ 和 $0\leqslant r\leqslant 2$。
步骤 4:转换为柱面坐标
将柱面坐标变换 $x=r\cos \theta$ 和 $y=r\sin \theta$ 代入积分区域,得到 $\dfrac {{x}^{2}+{y}^{2}}{4}\leqslant x\leqslant \sqrt {5-{x}^{2}-{y}^{2}}=\dfrac {{1}^{2}}{4}\leqslant x\leqslant \sqrt {5-{t}^{2}}$。
步骤 5:计算体积
利用柱面坐标计算体积,得到 $v= dv= 2π "dθ r2 rvs-2 r2 (√5-r^2-r^2/4)dr =π| 2 (√5-r^2-r/4 )d(r^2)]=2/3 π(5√5-4)$。