题目
曲线x=3t+1，x=3t+1，x=3t+1在x=3t+1点处的切线方程为(A)x=3t+1; (B)x=3t+1; (C)x=3t+1; (D)x=3t+1.
曲线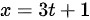
，
，
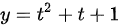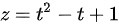在
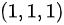点处的切线方程为
(A)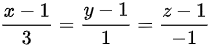
;
(B)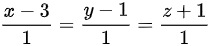
;
(C)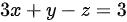
;
(D)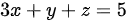
.
题目解答
答案
本题考查空间曲线.
.
.
.
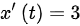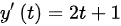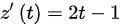令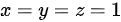
，解得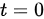
.
由参数方程切线公式，有切线方程为：
.
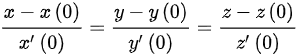代入相关数据，有：
.
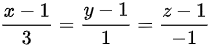故本题答案选A，排除B，C，D.
解析
步骤 1：求导数
对给定的参数方程求导，得到x'(t)，y'(t)，z'(t)。
x'(t) = 3.
y'(t) = 2t + 1.
z'(t) = 2t - 1.
步骤 2：确定参数值
将点(1,1,1)代入参数方程，求解t的值。
x = 3t + 1 = 1，解得t = 0.
步骤 3：计算切线方程
将t = 0代入x'(t)，y'(t)，z'(t)，得到切线的方向向量。
x'(0) = 3.
y'(0) = 1.
z'(0) = -1.
根据参数方程切线公式，有切线方程为：
$\dfrac {x-1}{3}=\dfrac {y-1}{1}=\dfrac {z-1}{-1}$.
对给定的参数方程求导，得到x'(t)，y'(t)，z'(t)。
x'(t) = 3.
y'(t) = 2t + 1.
z'(t) = 2t - 1.
步骤 2：确定参数值
将点(1,1,1)代入参数方程，求解t的值。
x = 3t + 1 = 1，解得t = 0.
步骤 3：计算切线方程
将t = 0代入x'(t)，y'(t)，z'(t)，得到切线的方向向量。
x'(0) = 3.
y'(0) = 1.
z'(0) = -1.
根据参数方程切线公式，有切线方程为：
$\dfrac {x-1}{3}=\dfrac {y-1}{1}=\dfrac {z-1}{-1}$.