题目
计算(int )_(0)^ln 2sqrt ({e)^x-1}dx时,常用换元法,若令(int )_(0)^ln 2sqrt ({e)^x-1}dx,则换元后定积分的下限与上限分别为( ) (int )_(0)^ln 2sqrt ({e)^x-1}dx (int )_(0)^ln 2sqrt ({e)^x-1}dx(int )_(0)^ln 2sqrt ({e)^x-1}dx(int )_(0)^ln 2sqrt ({e)^x-1}dx
计算 时,常用换元法,若令
时,常用换元法,若令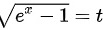 ,则换元后定积分的下限与上限分别为( )
,则换元后定积分的下限与上限分别为( )
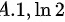
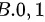
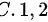

题目解答
答案
由题意得,
计算 时,常用换元法,若令
时,常用换元法,若令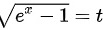 ,则
,则
当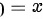 时,
时, ;
;
当 时,
时,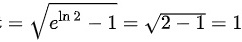 ;
;
故换元后定积分的下限与上限分别为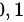 。
。
故答案选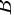 .
.
解析
步骤 1:确定原积分的上下限
原积分的下限为$x=0$,上限为$x=\ln 2$。
步骤 2:换元
令$\sqrt {{e}^{x}-1}=t$,则${e}^{x}-1={t}^{2}$,从而${e}^{x}={t}^{2}+1$。
步骤 3:计算换元后的下限
当$x=0$时,$t=\sqrt {{e}^{0}-1}=\sqrt {1-1}=0$。
步骤 4:计算换元后的上限
当$x=\ln 2$时,$t=\sqrt {{e}^{\ln 2}-1}=\sqrt {2-1}=1$。
原积分的下限为$x=0$,上限为$x=\ln 2$。
步骤 2:换元
令$\sqrt {{e}^{x}-1}=t$,则${e}^{x}-1={t}^{2}$,从而${e}^{x}={t}^{2}+1$。
步骤 3:计算换元后的下限
当$x=0$时,$t=\sqrt {{e}^{0}-1}=\sqrt {1-1}=0$。
步骤 4:计算换元后的上限
当$x=\ln 2$时,$t=\sqrt {{e}^{\ln 2}-1}=\sqrt {2-1}=1$。