题目
16.两台车床加工同样的零件,第一台出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍。(1)求任取一个零件是合格品的概率;(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率。
16.两台车床加工同样的零件,第一台出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍。
(1)求任取一个零件是合格品的概率;
(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率。
题目解答
答案
解:(1)设 表示第
表示第 台车床加工的零件,B表示合格品,由题可知:
台车床加工的零件,B表示合格品,由题可知:
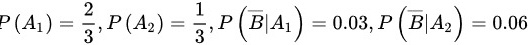
则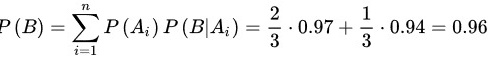
(2)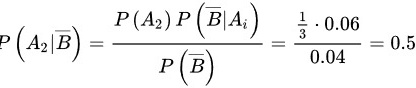
解析
考查要点:本题主要考查全概率公式和贝叶斯定理的应用,涉及条件概率的理解与计算。
解题核心思路:
- 确定各车床零件的比例:根据“第一台加工的零件比第二台多一倍”,确定第一台和第二台零件占总数的比例分别为$\dfrac{2}{3}$和$\dfrac{1}{3}$。
- 计算合格品概率:利用全概率公式,将两台车床的合格率按比例加权求和。
- 计算条件概率:在已知不合格品的条件下,用贝叶斯定理求出该零件来自第二台车床的概率。
破题关键点:
- 正确转换合格率与不合格率:合格率=1-不合格率。
- 区分总概率与条件概率:第二问需先求总不合格率,再用贝叶斯定理计算条件概率。
第(1)题
确定各车床零件比例
第一台加工的零件占$\dfrac{2}{3}$,第二台占$\dfrac{1}{3}$。
计算各车床合格率
- 第一台合格率:$1 - 0.03 = 0.97$
- 第二台合格率:$1 - 0.06 = 0.94$
应用全概率公式
总合格率:
$P(B) = \dfrac{2}{3} \cdot 0.97 + \dfrac{1}{3} \cdot 0.94 = 0.96$
第(2)题
计算总不合格率
总不合格率:
$P(\overline{B}) = 1 - P(B) = 1 - 0.96 = 0.04$
计算第二台的不合格贡献
第二台不合格品的概率:
$P(A_2 \cap \overline{B}) = \dfrac{1}{3} \cdot 0.06 = 0.02$
应用贝叶斯定理
条件概率:
$P(A_2 \mid \overline{B}) = \dfrac{P(A_2 \cap \overline{B})}{P(\overline{B})} = \dfrac{0.02}{0.04} = 0.5$