求方程组的通解 =x+y dfrac {dy)(dt)=2y ..
求方程组的通解 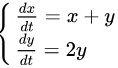 .
.
题目解答
答案
由题意,方程组 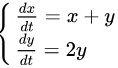 ,
,
则可得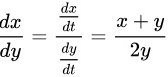 ,
,
整理得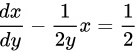 ,这是一个一阶线性微分方程,利用一阶线性微分方程的通解公式可得方程的通解
,这是一个一阶线性微分方程,利用一阶线性微分方程的通解公式可得方程的通解
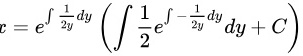
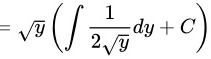
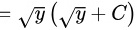
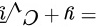 ,C为任意常数.
,C为任意常数.
所以方程组的通解为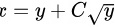 .
.
故答案为: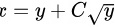
解析
考查要点:本题主要考查常微分方程组的解法,特别是通过消元法将方程组转化为一阶线性微分方程,并利用积分因子法求解。
解题核心思路:
- 消去参数$t$:通过将两个微分方程相除,得到$\dfrac{dx}{dy}$,从而消去时间变量$t$,将方程组转化为关于$x$和$y$的微分方程。
- 识别方程类型:将方程整理为一阶线性微分方程的标准形式$\dfrac{dx}{dy} + P(y)x = Q(y)$。
- 应用积分因子法:通过计算积分因子,求解通解。
破题关键点:
- 正确消元:利用$\dfrac{dx}{dt} / \dfrac{dy}{dt} = \dfrac{dx}{dy}$,前提是$\dfrac{dy}{dt} \neq 0$。
- 积分因子的计算:准确计算积分因子$\mu(y) = e^{\int -\dfrac{1}{2y} dy}$。
步骤1:消去参数$t$
由方程组:
$\begin{cases}\dfrac{dx}{dt} = x + y \\\dfrac{dy}{dt} = 2y\end{cases}$
将两式相除,消去$dt$:
$\dfrac{dx}{dy} = \dfrac{\dfrac{dx}{dt}}{\dfrac{dy}{dt}} = \dfrac{x + y}{2y}.$
步骤2:整理为一阶线性方程
将方程变形为:
$\dfrac{dx}{dy} - \dfrac{1}{2y}x = \dfrac{1}{2}.$
此时方程符合标准形式$\dfrac{dx}{dy} + P(y)x = Q(y)$,其中:
$P(y) = -\dfrac{1}{2y}, \quad Q(y) = \dfrac{1}{2}.$
步骤3:计算积分因子
积分因子为:
$\mu(y) = e^{\int P(y) dy} = e^{\int -\dfrac{1}{2y} dy} = e^{-\dfrac{1}{2} \ln y} = y^{-\dfrac{1}{2}} = \dfrac{1}{\sqrt{y}}.$
步骤4:应用通解公式
通解公式为:
$x = \dfrac{1}{\mu(y)} \left( \int \mu(y) Q(y) dy + C \right).$
代入$\mu(y)$和$Q(y)$:
$x = \sqrt{y} \left( \int \dfrac{1}{2\sqrt{y}} dy + C \right).$
步骤5:计算积分并化简
计算积分:
$\int \dfrac{1}{2\sqrt{y}} dy = \sqrt{y} + C.$
代入通解公式:
$x = \sqrt{y} \cdot (\sqrt{y} + C) = y + C\sqrt{y}.$