题目
不定积分int dfrac (1)(1+sqrt {1-x)}dx=( ) int dfrac (1)(1+sqrt {1-x)}dx=int dfrac (1)(1+sqrt {1-x)}dx=int dfrac (1)(1+sqrt {1-x)}dx=int dfrac (1)(1+sqrt {1-x)}dx=
不定积分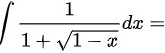 ( )
( )
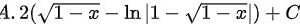
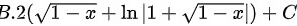
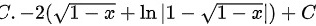
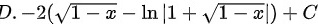
题目解答
答案
由题意得,
利用换元积分法有,
可令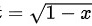 ,则
,则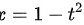 ,
,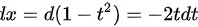 ,
,
故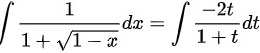
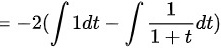
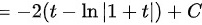
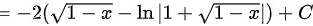 。
。
故答案选 .
.
解析
步骤 1:换元积分法
令$t=\sqrt{1-x}$,则$x=1-t^2$,$dx=-2tdt$。
步骤 2:代入积分
将$t$和$dx$代入原积分,得到$\int \dfrac{-2t}{1+t}dt$。
步骤 3:分部积分
将$\int \dfrac{-2t}{1+t}dt$拆分为$-2\int 1dt + 2\int \dfrac{1}{1+t}dt$。
步骤 4:计算积分
$-2\int 1dt = -2t$,$2\int \dfrac{1}{1+t}dt = 2\ln|1+t|$。
步骤 5:代回原变量
将$t$代回原变量$x$,得到$-2(\sqrt{1-x}-\ln|1+\sqrt{1-x}|)+C$。
令$t=\sqrt{1-x}$,则$x=1-t^2$,$dx=-2tdt$。
步骤 2:代入积分
将$t$和$dx$代入原积分,得到$\int \dfrac{-2t}{1+t}dt$。
步骤 3:分部积分
将$\int \dfrac{-2t}{1+t}dt$拆分为$-2\int 1dt + 2\int \dfrac{1}{1+t}dt$。
步骤 4:计算积分
$-2\int 1dt = -2t$,$2\int \dfrac{1}{1+t}dt = 2\ln|1+t|$。
步骤 5:代回原变量
将$t$代回原变量$x$,得到$-2(\sqrt{1-x}-\ln|1+\sqrt{1-x}|)+C$。