题目

下列不定积分的基本公式不正确的是. A int cos xdx=sin x+CB int cos xdx=sin x+CC int cos xdx=sin x+CD int cos xdx=sin x+C

下列不定积分的基本公式不正确的是.

A 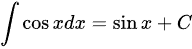$\int_{ }^{ }\cos xdx=\sin x+C$

B 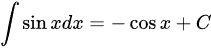$\int_{ }^{ }\sin xdx=-\c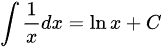os x+C$

C $\int_{ }^{ }\frac{1}{x}d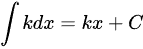x=\ln x+C$

D $\int_{ }^{ }kdx=kx+C$

题目解答

答案

选项A：

对等式两边求导，易得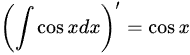 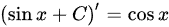$\left(\int_{ }^{ }\cos xdx\right)'=\cos x$ ， $\left(\sin x+C\right)'=\cos x$ ；左右相等，选项正确

选项B：

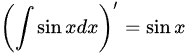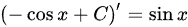左右两边求导，得 $\left(\int_{ }^{ }\sin xdx\right)'=\sin x$ ，

$\left(-\cos x+C\right)'=\sin x$ ，选项正确；

选项C：

由积分公式，易得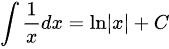 $\int_{ }^{ }\frac{1}{x}dx=\ln\left|x\right|+C$

因此选项错误；

选项D：

由积分公式，易得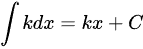 $\int_{ }^{ }kdx=kx+C$ ，因此选项正确.

解析

步骤 1：验证选项A
对等式两边求导，易得$(\int \cos xdx)'=\cos x$，$(\sin x+C)'=\cos x$；左右相等，选项正确。
步骤 2：验证选项B
左右两边求导，得$(\int \sin xdx)'=\sin x$，$(-\cos x+C)'=\sin x$，选项正确。
步骤 3：验证选项C
由积分公式，易得$\int \dfrac {1}{x}dx=\ln |x|+C$，因此选项错误。
步骤 4：验证选项D
由积分公式，易得kdx=kx+C，因此选项正确。