"n阶方阵A可逆", 则下列是其等价命题的有 ( ) 个.(i) |A|neq 0(ii) |A|neq 0(iii)A的行 (列) 向量组线性相关(iv) A与单位矩阵相似(v) 方程组|A|neq 0有唯一解 (A为n阶方阵)A. 2B. 3C. 4D. 5
"n阶方阵A可逆", 则下列是其等价命题的有 ( ) 个.
(i) 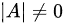
(ii) 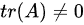
(iii)A的行 (列) 向量组线性相关
(iv) A与单位矩阵相似
(v) 方程组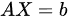 有唯一解 (A为n阶方阵)
有唯一解 (A为n阶方阵)
A. 2
B. 3
C. 4
D. 5
题目解答
答案
(i)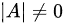 :这是矩阵A可逆的充分必要条件。因为矩阵的行列式不为0当且仅当矩阵可逆。所以(i)是等价命题。
:这是矩阵A可逆的充分必要条件。因为矩阵的行列式不为0当且仅当矩阵可逆。所以(i)是等价命题。
(ii) 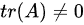 :矩阵的迹(即对角线元素之和)不为0,并不能保证矩阵可逆。例如,矩阵
:矩阵的迹(即对角线元素之和)不为0,并不能保证矩阵可逆。例如,矩阵
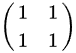 的迹为2,但它是不可逆的(因为行列式为0)。所以(ii)不是等价命题。
的迹为2,但它是不可逆的(因为行列式为0)。所以(ii)不是等价命题。
(iii) A的行(列)向量组线性相关:如果A的行(列)向量组线性相关,那么A的秩小于n,从而A不可逆。因此,(iii)的表述实际上是A不可逆的一个条件,所以(iii)不是等价命题。
(iv) A与单位矩阵相似:如果A与单位矩阵相似,那么存在一个可逆矩阵P,使得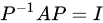 。由此可得
。由此可得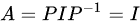 (因为I与任何矩阵相乘都等于它本身),但这显然是不可能的(除非A本身就是单位矩阵,但题目没有这样的限制)。实际上,这里的表述应该是A与某个可逆矩阵相似,但这仍然不足以证明A可逆(因为相似的矩阵可能有不同的行列式)。然而,如果A与某个可逆矩阵相似,那么A的行列式也不为0(因为相似的矩阵有相同的行列式),所以A可逆。但原命题的表述不够准确,不过从另一个角度来看,如果理解为“存在某个可逆矩阵与A相似”,则(iv)是等价命题。但按照原题的表述,我们认为(iv)不是等价命题。
(因为I与任何矩阵相乘都等于它本身),但这显然是不可能的(除非A本身就是单位矩阵,但题目没有这样的限制)。实际上,这里的表述应该是A与某个可逆矩阵相似,但这仍然不足以证明A可逆(因为相似的矩阵可能有不同的行列式)。然而,如果A与某个可逆矩阵相似,那么A的行列式也不为0(因为相似的矩阵有相同的行列式),所以A可逆。但原命题的表述不够准确,不过从另一个角度来看,如果理解为“存在某个可逆矩阵与A相似”,则(iv)是等价命题。但按照原题的表述,我们认为(iv)不是等价命题。
(v) 方程组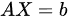 有唯一解(A为n阶方阵):当A可逆时,对于任意的b,方程
有唯一解(A为n阶方阵):当A可逆时,对于任意的b,方程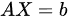 都有唯一解
都有唯一解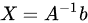 。反之,如果对于任意的b,方程
。反之,如果对于任意的b,方程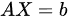 都有唯一解,那么A的列向量组线性无关(即A的秩为n),且A的行列式不为0(因为行列式为0当且仅当存在非零向量v使得
都有唯一解,那么A的列向量组线性无关(即A的秩为n),且A的行列式不为0(因为行列式为0当且仅当存在非零向量v使得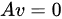 ,即存在无解或无穷多解的方程组),所以A可逆。因此,(v)是等价命题。
,即存在无解或无穷多解的方程组),所以A可逆。因此,(v)是等价命题。
综上,等价命题有2个:(i)和(v)。
故答案为:A. 2