题目
计算∥x^2+y^2)dS,其中 Z 是锥面∥x^2+y^2)dS,被平面 z = 3 所截的部分
计算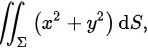
其中 Z 是锥面
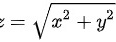被平面 z = 3 所截的部分
题目解答
答案
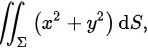
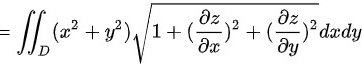
其中
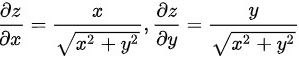
则有
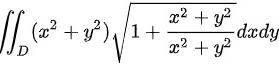
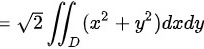
D: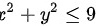
令
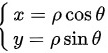,其中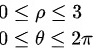
原式=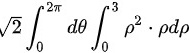
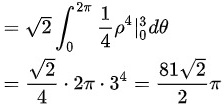
解析
步骤 1：确定积分区域
锥面$z=\sqrt {{x}^{2}+{y}^{2}}$被平面$z=3$所截的部分，即$z=3$时，有$\sqrt {{x}^{2}+{y}^{2}}=3$，因此$x^2+y^2=9$。这表示积分区域D是一个半径为3的圆。
步骤 2：计算曲面的微分面积
曲面$z=\sqrt {{x}^{2}+{y}^{2}}$的微分面积$dS$可以通过计算$\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}dxdy$得到。其中$\frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^2+y^2}}$，$\frac{\partial z}{\partial y}=\frac{y}{\sqrt{x^2+y^2}}$。因此，$dS=\sqrt{1+\frac{x^2}{x^2+y^2}+\frac{y^2}{x^2+y^2}}dxdy=\sqrt{2}dxdy$。
步骤 3：转换为极坐标并计算积分
将$x^2+y^2$转换为极坐标形式，即$r^2$，其中$r$是极径，$dxdy=rdrd\theta$。因此，原积分可以转换为$\sqrt{2}\int_{0}^{2\pi}\int_{0}^{3}r^3drd\theta$。
步骤 4：计算积分
$\sqrt{2}\int_{0}^{2\pi}\int_{0}^{3}r^3drd\theta=\sqrt{2}\int_{0}^{2\pi}[\frac{r^4}{4}]_{0}^{3}d\theta=\sqrt{2}\int_{0}^{2\pi}\frac{81}{4}d\theta=\frac{81\sqrt{2}}{4}\int_{0}^{2\pi}d\theta=\frac{81\sqrt{2}}{4}\cdot2\pi=\frac{81\sqrt{2}\pi}{2}$。
锥面$z=\sqrt {{x}^{2}+{y}^{2}}$被平面$z=3$所截的部分，即$z=3$时，有$\sqrt {{x}^{2}+{y}^{2}}=3$，因此$x^2+y^2=9$。这表示积分区域D是一个半径为3的圆。
步骤 2：计算曲面的微分面积
曲面$z=\sqrt {{x}^{2}+{y}^{2}}$的微分面积$dS$可以通过计算$\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}dxdy$得到。其中$\frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^2+y^2}}$，$\frac{\partial z}{\partial y}=\frac{y}{\sqrt{x^2+y^2}}$。因此，$dS=\sqrt{1+\frac{x^2}{x^2+y^2}+\frac{y^2}{x^2+y^2}}dxdy=\sqrt{2}dxdy$。
步骤 3：转换为极坐标并计算积分
将$x^2+y^2$转换为极坐标形式，即$r^2$，其中$r$是极径，$dxdy=rdrd\theta$。因此，原积分可以转换为$\sqrt{2}\int_{0}^{2\pi}\int_{0}^{3}r^3drd\theta$。
步骤 4：计算积分
$\sqrt{2}\int_{0}^{2\pi}\int_{0}^{3}r^3drd\theta=\sqrt{2}\int_{0}^{2\pi}[\frac{r^4}{4}]_{0}^{3}d\theta=\sqrt{2}\int_{0}^{2\pi}\frac{81}{4}d\theta=\frac{81\sqrt{2}}{4}\int_{0}^{2\pi}d\theta=\frac{81\sqrt{2}}{4}\cdot2\pi=\frac{81\sqrt{2}\pi}{2}$。