题目
7.设随机变量X的概率密度为 f(x)= ) x,0lt xleqslant 1; 2-x,1lt xleqslant 2; 0, 的值是 () .-|||-A.0.5 B.0.6 C.0.66 D.0.7

题目解答
答案
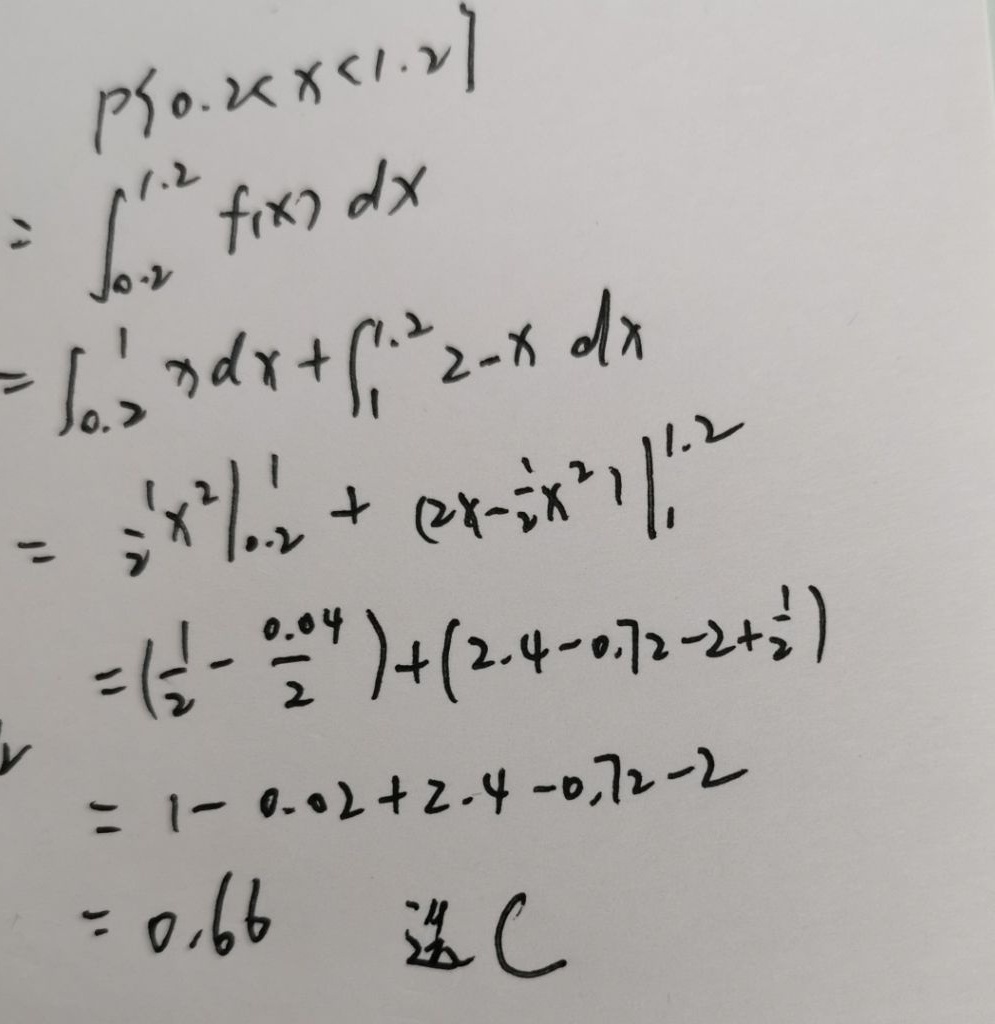
解析
步骤 1:确定积分区间
根据题目,$P\{ 0.2\lt X\lt 1.2\} $ 的计算需要将积分区间分为两部分,即 $0.2\lt x\leqslant 1$ 和 $1\lt x\lt 1.2$,因为概率密度函数在 $x=1$ 处有不同的表达式。
步骤 2:计算第一部分的积分
在区间 $0.2\lt x\leqslant 1$ 上,概率密度函数为 $f(x)=x$,因此需要计算 ${\int }_{0.2}^{1}xdx$。
步骤 3:计算第二部分的积分
在区间 $1\lt x\lt 1.2$ 上,概率密度函数为 $f(x)=2-x$,因此需要计算 ${\int }_{1}^{1.2}(2-x)dx$。
步骤 4:求和
将步骤 2 和步骤 3 的结果相加,得到 $P\{ 0.2\lt X\lt 1.2\} $ 的值。
根据题目,$P\{ 0.2\lt X\lt 1.2\} $ 的计算需要将积分区间分为两部分,即 $0.2\lt x\leqslant 1$ 和 $1\lt x\lt 1.2$,因为概率密度函数在 $x=1$ 处有不同的表达式。
步骤 2:计算第一部分的积分
在区间 $0.2\lt x\leqslant 1$ 上,概率密度函数为 $f(x)=x$,因此需要计算 ${\int }_{0.2}^{1}xdx$。
步骤 3:计算第二部分的积分
在区间 $1\lt x\lt 1.2$ 上,概率密度函数为 $f(x)=2-x$,因此需要计算 ${\int }_{1}^{1.2}(2-x)dx$。
步骤 4:求和
将步骤 2 和步骤 3 的结果相加,得到 $P\{ 0.2\lt X\lt 1.2\} $ 的值。