题目
具有n个顶点的完全图,其边的总数为 __-|||-(A) dfrac (n!)(2) (B) dfrac (n(n-1))(2)-|||-(C) dfrac ({n)^2}(2) (D) dfrac ({n)^2}(2)-1

题目解答
答案
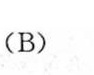
解析
步骤 1:理解完全图的定义
完全图是指图中任意两个顶点之间都有一条边相连的图。因此,每个顶点都与其他n-1个顶点相连。
步骤 2:计算边的总数
由于每个顶点都与其他n-1个顶点相连,所以每个顶点贡献n-1条边。但是,每条边都被计算了两次(一次从一个顶点到另一个顶点,一次从另一个顶点到这个顶点),因此,边的总数为$\dfrac{n(n-1)}{2}$。
步骤 3:选择正确答案
根据上述计算,边的总数为$\dfrac{n(n-1)}{2}$,因此,正确答案为(B)。
完全图是指图中任意两个顶点之间都有一条边相连的图。因此,每个顶点都与其他n-1个顶点相连。
步骤 2:计算边的总数
由于每个顶点都与其他n-1个顶点相连,所以每个顶点贡献n-1条边。但是,每条边都被计算了两次(一次从一个顶点到另一个顶点,一次从另一个顶点到这个顶点),因此,边的总数为$\dfrac{n(n-1)}{2}$。
步骤 3:选择正确答案
根据上述计算,边的总数为$\dfrac{n(n-1)}{2}$,因此,正确答案为(B)。