题目
设随机变量的概率密度函数为:求的概率密度函数。
设随机变量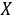 的概率密度函数为:
的概率密度函数为:
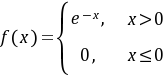
求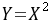 的概率密度函数。
的概率密度函数。
题目解答
答案
解: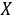 的分布函数
的分布函数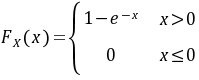 ,
,
当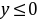 时
时
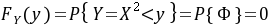 ,
,
当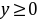 时,
时,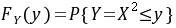
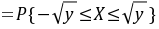
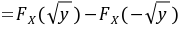
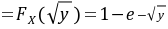
所以,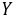 的概率密度为
的概率密度为
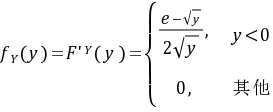
解析
步骤 1:确定随机变量X的分布函数
给定随机变量X的概率密度函数$f(x)$,我们首先确定其分布函数$F_X(x)$。根据定义,分布函数$F_X(x)$是概率密度函数$f(x)$的积分,即$F_X(x) = \int_{-\infty}^{x} f(t) dt$。对于给定的概率密度函数$f(x)$,我们有:
$$
F_X(x) = \left\{
\begin{array}{ll}
0 & \text{if } x \leq 0 \\
1 - e^{-x} & \text{if } x > 0
\end{array}
\right.
$$
步骤 2:确定随机变量Y的分布函数
随机变量Y定义为$Y = X^2$。为了找到Y的分布函数$F_Y(y)$,我们需要考虑$Y \leq y$的概率,即$P(Y \leq y) = P(X^2 \leq y)$。由于$X^2$是非负的,我们只需要考虑$y \geq 0$的情况。对于$y \geq 0$,我们有:
$$
F_Y(y) = P(X^2 \leq y) = P(-\sqrt{y} \leq X \leq \sqrt{y})
$$
由于$X$的分布函数$F_X(x)$在$x \leq 0$时为0,我们只需要考虑$X$在$[0, \sqrt{y}]$区间内的分布,即:
$$
F_Y(y) = F_X(\sqrt{y}) - F_X(-\sqrt{y}) = F_X(\sqrt{y}) = 1 - e^{-\sqrt{y}}
$$
步骤 3:确定随机变量Y的概率密度函数
随机变量Y的概率密度函数$f_Y(y)$是分布函数$F_Y(y)$的导数,即$f_Y(y) = \frac{d}{dy} F_Y(y)$。根据步骤2中的$F_Y(y)$,我们有:
$$
f_Y(y) = \frac{d}{dy} (1 - e^{-\sqrt{y}}) = \frac{e^{-\sqrt{y}}}{2\sqrt{y}}
$$
给定随机变量X的概率密度函数$f(x)$,我们首先确定其分布函数$F_X(x)$。根据定义,分布函数$F_X(x)$是概率密度函数$f(x)$的积分,即$F_X(x) = \int_{-\infty}^{x} f(t) dt$。对于给定的概率密度函数$f(x)$,我们有:
$$
F_X(x) = \left\{
\begin{array}{ll}
0 & \text{if } x \leq 0 \\
1 - e^{-x} & \text{if } x > 0
\end{array}
\right.
$$
步骤 2:确定随机变量Y的分布函数
随机变量Y定义为$Y = X^2$。为了找到Y的分布函数$F_Y(y)$,我们需要考虑$Y \leq y$的概率,即$P(Y \leq y) = P(X^2 \leq y)$。由于$X^2$是非负的,我们只需要考虑$y \geq 0$的情况。对于$y \geq 0$,我们有:
$$
F_Y(y) = P(X^2 \leq y) = P(-\sqrt{y} \leq X \leq \sqrt{y})
$$
由于$X$的分布函数$F_X(x)$在$x \leq 0$时为0,我们只需要考虑$X$在$[0, \sqrt{y}]$区间内的分布,即:
$$
F_Y(y) = F_X(\sqrt{y}) - F_X(-\sqrt{y}) = F_X(\sqrt{y}) = 1 - e^{-\sqrt{y}}
$$
步骤 3:确定随机变量Y的概率密度函数
随机变量Y的概率密度函数$f_Y(y)$是分布函数$F_Y(y)$的导数,即$f_Y(y) = \frac{d}{dy} F_Y(y)$。根据步骤2中的$F_Y(y)$,我们有:
$$
f_Y(y) = \frac{d}{dy} (1 - e^{-\sqrt{y}}) = \frac{e^{-\sqrt{y}}}{2\sqrt{y}}
$$