题目
设A为3阶矩阵,A的特征值为1,2,2,则(A)^-1-E|= ( )A 5 B 4 C 1 D 0
设A为3阶矩阵,A的特征值为1,2,2,则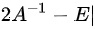
= ( )
A 5
B 4
C 1
D 0
题目解答
答案
由A为3阶矩阵,A的特征值为1,2,2可得，对应2A^{-1}-E的特征值为：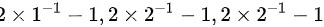
即1，0，0
由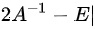等于3个特征值相乘，故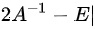=0，即本题选D
解析
步骤 1：确定矩阵A的特征值
已知矩阵A的特征值为1, 2, 2。
步骤 2：计算矩阵$2{A}^{-1}-E$的特征值
对于矩阵A的特征值$\lambda$，矩阵$2{A}^{-1}-E$的特征值为$2\lambda^{-1}-1$。
- 对于特征值1，$2{1}^{-1}-1=2-1=1$。
- 对于特征值2，$2{2}^{-1}-1=1-1=0$。
- 对于特征值2，$2{2}^{-1}-1=1-1=0$。
因此，矩阵$2{A}^{-1}-E$的特征值为1, 0, 0。
步骤 3：计算矩阵$2{A}^{-1}-E$的行列式
矩阵的行列式等于其特征值的乘积。因此，$2{A}^{-1}-E|$=1×0×0=0。
已知矩阵A的特征值为1, 2, 2。
步骤 2：计算矩阵$2{A}^{-1}-E$的特征值
对于矩阵A的特征值$\lambda$，矩阵$2{A}^{-1}-E$的特征值为$2\lambda^{-1}-1$。
- 对于特征值1，$2{1}^{-1}-1=2-1=1$。
- 对于特征值2，$2{2}^{-1}-1=1-1=0$。
- 对于特征值2，$2{2}^{-1}-1=1-1=0$。
因此，矩阵$2{A}^{-1}-E$的特征值为1, 0, 0。
步骤 3：计算矩阵$2{A}^{-1}-E$的行列式
矩阵的行列式等于其特征值的乘积。因此，$2{A}^{-1}-E|$=1×0×0=0。