题目
非齐次线性方程组-2(x)_(1)+(x)_(2)+(x)_(3)=-2-|||-__ __-|||-_(1)-2(x)_(2)+(x)_(3)=lambda -|||-【_(1)+(x)_(2)-2(x)_(3)=(lambda )^2-|||-__当-2(x)_(1)+(x)_(2)+(x)_(3)=-2-|||-__ __-|||-_(1)-2(x)_(2)+(x)_(3)=lambda -|||-【_(1)+(x)_(2)-2(x)_(3)=(lambda )^2-|||-__取何值时有解?并求出他的通解。
非齐次线性方程组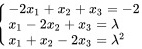 当
当 取何值时有解?并求出他的通解。
取何值时有解?并求出他的通解。
题目解答
答案

解析
步骤 1:写出增广矩阵
将非齐次线性方程组写成增广矩阵的形式,即
$$
B = \left(\begin{matrix}
-2 & 1 & 1 & -2 \\
1 & -2 & 1 & \lambda \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
步骤 2:进行初等行变换
对增广矩阵进行初等行变换,以简化矩阵。首先,将第一行与第二行交换,得到
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
-2 & 1 & 1 & -2 \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
然后,对第二行进行变换,使其第一列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & -3 & 3 & -2+2\lambda \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
接着,对第三行进行变换,使其第一列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & -3 & 3 & -2+2\lambda \\
0 & 3 & -3 & \lambda^2-\lambda
\end{matrix}\right)
$$
步骤 3:继续进行初等行变换
对第二行进行变换,使其第二列元素为1,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & 1 & -1 & \frac{2}{3}(1-\lambda) \\
0 & 3 & -3 & \lambda^2-\lambda
\end{matrix}\right)
$$
然后,对第三行进行变换,使其第二列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & 1 & -1 & \frac{2}{3}(1-\lambda) \\
0 & 0 & 0 & (\lambda-1)(\lambda+2)
\end{matrix}\right)
$$
步骤 4:分析方程组的解
根据增广矩阵的最终形式,可以看出方程组有解的条件是$(\lambda-1)(\lambda+2)=0$,即$\lambda=1$或$\lambda=-2$。
步骤 5:求解方程组
当$\lambda=1$时,方程组变为
$$
\left\{\begin{matrix}
-2x_1+x_2+x_3=-2\\
x_1-2x_2+x_3=1\\
x_1+x_2-2x_3=1
\end{matrix}\right.
$$
解得$x_1=0$,$x_2=0$,$x_3=-2$,即方程组的解为$(0,0,-2)$。
当$\lambda=-2$时,方程组变为
$$
\left\{\begin{matrix}
-2x_1+x_2+x_3=-2\\
x_1-2x_2+x_3=-2\\
x_1+x_2-2x_3=4
\end{matrix}\right.
$$
解得$x_1=0$,$x_2=0$,$x_3=-2$,即方程组的解为$(0,0,-2)$。
将非齐次线性方程组写成增广矩阵的形式,即
$$
B = \left(\begin{matrix}
-2 & 1 & 1 & -2 \\
1 & -2 & 1 & \lambda \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
步骤 2:进行初等行变换
对增广矩阵进行初等行变换,以简化矩阵。首先,将第一行与第二行交换,得到
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
-2 & 1 & 1 & -2 \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
然后,对第二行进行变换,使其第一列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & -3 & 3 & -2+2\lambda \\
1 & 1 & -2 & \lambda^2
\end{matrix}\right)
$$
接着,对第三行进行变换,使其第一列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & -3 & 3 & -2+2\lambda \\
0 & 3 & -3 & \lambda^2-\lambda
\end{matrix}\right)
$$
步骤 3:继续进行初等行变换
对第二行进行变换,使其第二列元素为1,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & 1 & -1 & \frac{2}{3}(1-\lambda) \\
0 & 3 & -3 & \lambda^2-\lambda
\end{matrix}\right)
$$
然后,对第三行进行变换,使其第二列元素为0,即
$$
B = \left(\begin{matrix}
1 & -2 & 1 & \lambda \\
0 & 1 & -1 & \frac{2}{3}(1-\lambda) \\
0 & 0 & 0 & (\lambda-1)(\lambda+2)
\end{matrix}\right)
$$
步骤 4:分析方程组的解
根据增广矩阵的最终形式,可以看出方程组有解的条件是$(\lambda-1)(\lambda+2)=0$,即$\lambda=1$或$\lambda=-2$。
步骤 5:求解方程组
当$\lambda=1$时,方程组变为
$$
\left\{\begin{matrix}
-2x_1+x_2+x_3=-2\\
x_1-2x_2+x_3=1\\
x_1+x_2-2x_3=1
\end{matrix}\right.
$$
解得$x_1=0$,$x_2=0$,$x_3=-2$,即方程组的解为$(0,0,-2)$。
当$\lambda=-2$时,方程组变为
$$
\left\{\begin{matrix}
-2x_1+x_2+x_3=-2\\
x_1-2x_2+x_3=-2\\
x_1+x_2-2x_3=4
\end{matrix}\right.
$$
解得$x_1=0$,$x_2=0$,$x_3=-2$,即方程组的解为$(0,0,-2)$。