题目
函数=x(y)^2(z)^2在点=x(y)^2(z)^2处沿其梯度方向的方向导数为( )。A.1B.2C.3D.4
函数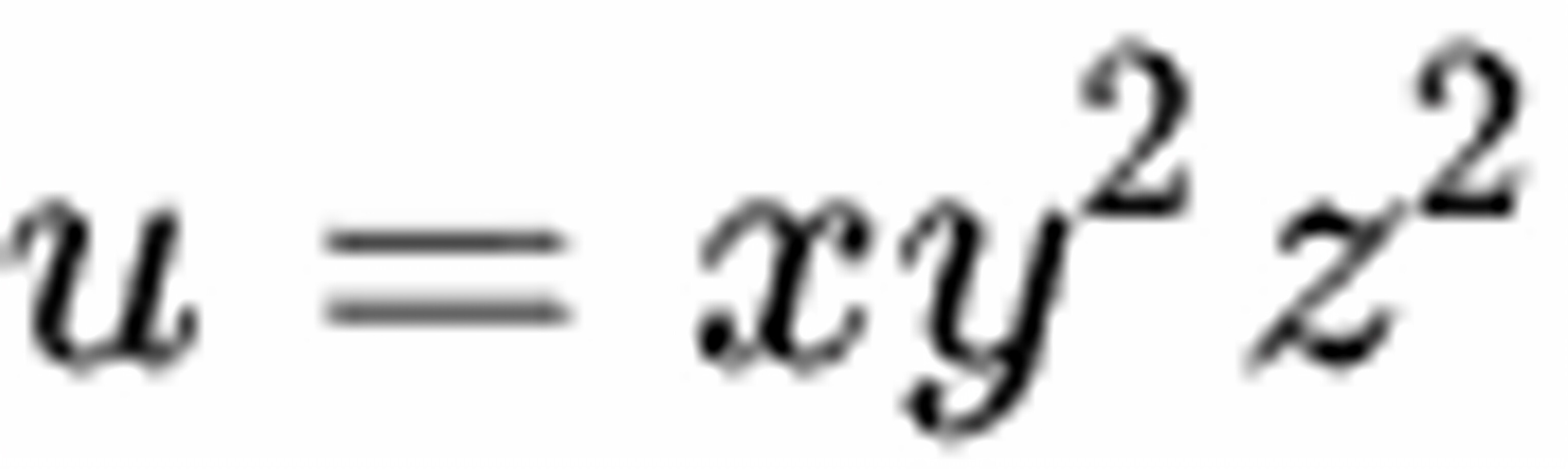 在点
在点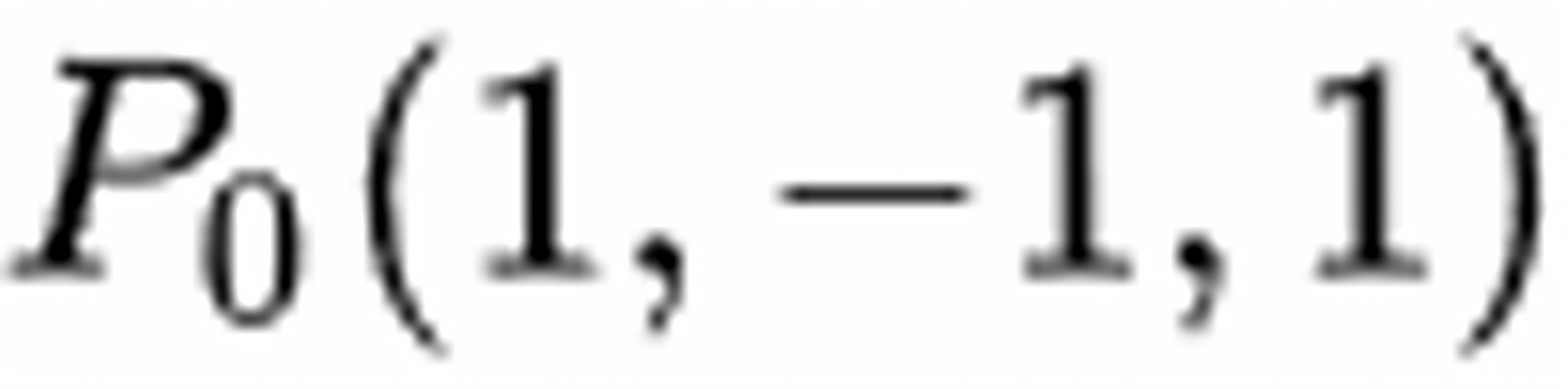 处沿其梯度方向的方向导数为( )。
处沿其梯度方向的方向导数为( )。
A.1
B.2
C.3
D.4
题目解答
答案
由题意知,对函数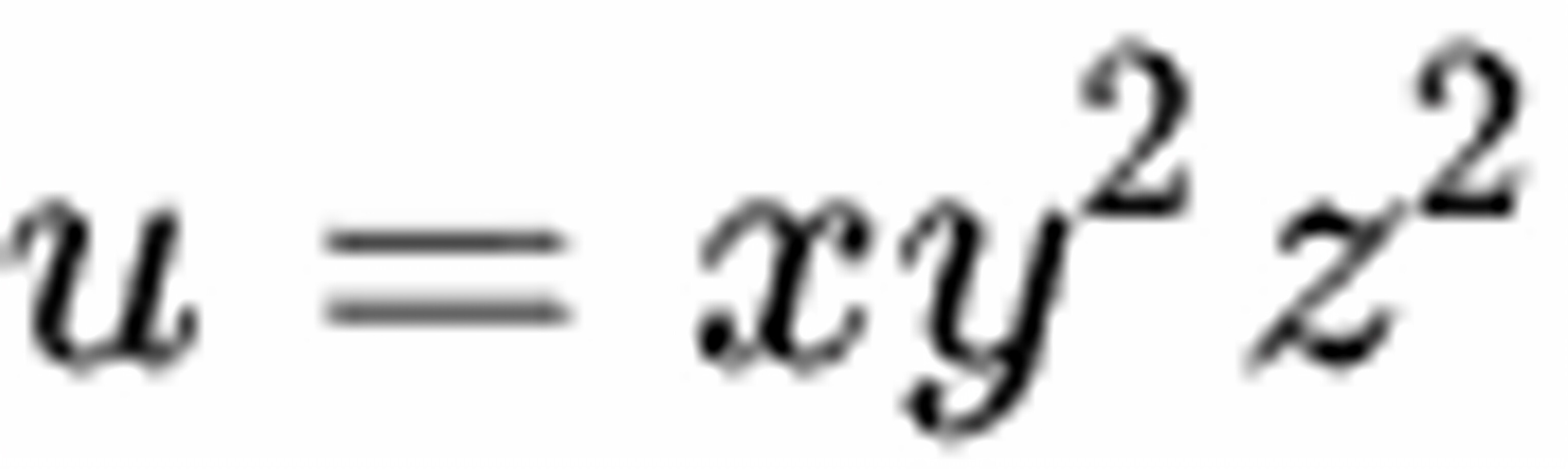 求x,y,z的偏导数得
求x,y,z的偏导数得
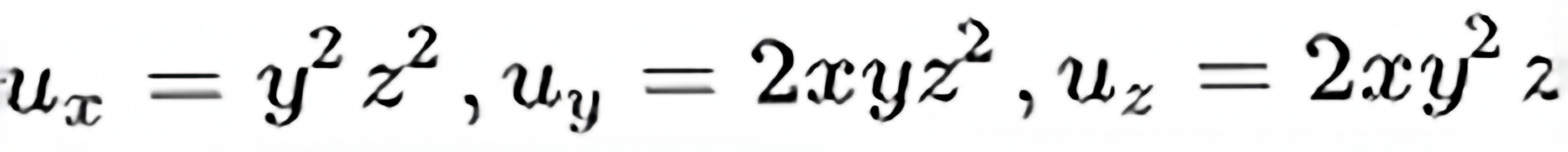
将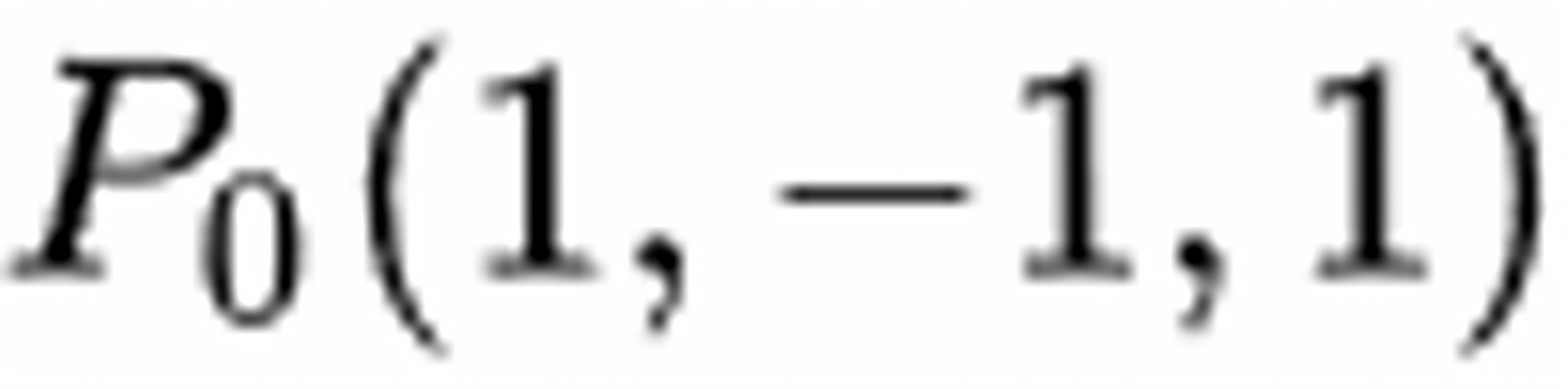 代入得
代入得
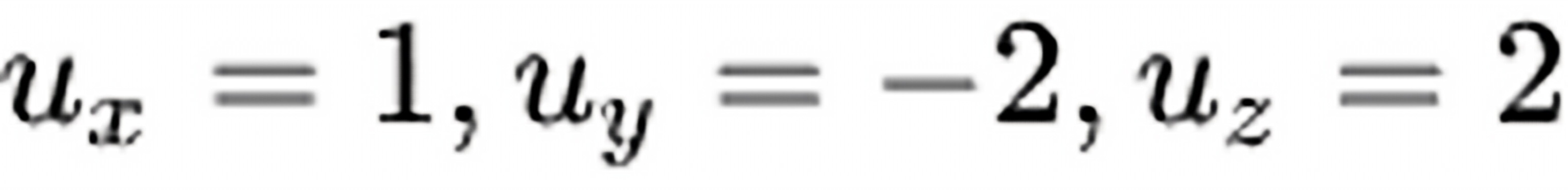
则沿其梯度方向的方向导数为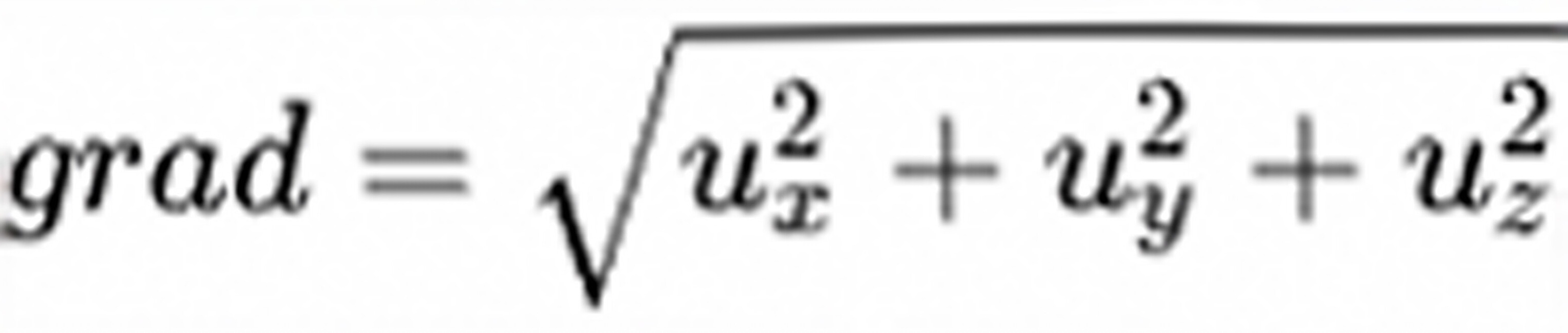
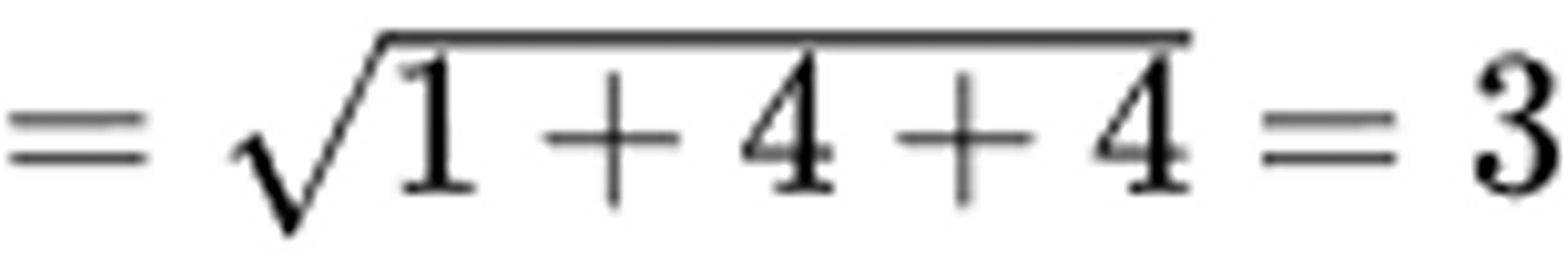
故答案选D。
解析
考查要点:本题主要考查梯度的计算以及方向导数的性质,特别是沿梯度方向的方向导数的求解方法。
解题核心思路:
- 梯度向量由函数在各变量方向的偏导数组成,其方向是函数值增长最快的方向。
- 方向导数的大小等于梯度向量在该方向上的投影。沿梯度方向的方向导数最大,且等于梯度的模长。
破题关键点:
- 正确计算函数在点$P_0$处的偏导数,得到梯度向量。
- 计算梯度向量的模长,即为所求的方向导数。
步骤1:计算偏导数
函数$u = x y^2 z^2$的偏导数为:
- 对$x$偏导:$\frac{\partial u}{\partial x} = y^2 z^2$
- 对$y$偏导:$\frac{\partial u}{\partial y} = 2x y z^2$
- 对$z$偏导:$\frac{\partial u}{\partial z} = 2x y^2 z$
步骤2:代入点$P_0(1, -1, 1)$
- $\frac{\partial u}{\partial x} = (-1)^2 \cdot 1^2 = 1$
- $\frac{\partial u}{\partial y} = 2 \cdot 1 \cdot (-1) \cdot 1^2 = -2$
- $\frac{\partial u}{\partial z} = 2 \cdot 1 \cdot (-1)^2 \cdot 1 = 2$
步骤3:计算梯度模长
梯度向量为$(1, -2, 2)$,其模长为:
$\sqrt{1^2 + (-2)^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3$
结论:沿梯度方向的方向导数为$3$,对应选项D。